最小生成树算法适用于无向图。最小生成树算法旨在求解无向图中所有结点的最小生成树,即所有结点的最小连通子图。最小生成树算法一般不适用于有向图。
在无向图中,一条边的两个端点都是可以互相到达的,所以我们可以将一条边看作是两个结点之间的一条双向边。而在有向图中,一条边的两个端点之间的连通情况并不一定是可以互相到达的。所以,最小生成树算法不适用于有向图。
树、
如果一个无向连通图G中不存在回路,则称图G是一颗树。
生成树(可以带权也可以不带权)、
一个连通图的生成树是一个极小的连通子图,它包含图中全部的 n 个顶点,但只有构成一棵树的n-1条边。
生成树的属性:
- 一个连通图可以有多个生成树;
- 一个连通图的所有生成树都包含相同的顶点个数和边数;
- 生成树当中不存在环;
- 移除生成树中的任意一条边都会导致图的不连通, 生成树的边最少特性;
- 在生成树中添加一条边会构成环。
- 对于包含n个顶点的连通图,生成树包含n个顶点和n-1条边;
- 对于包含n个顶点的无向完全图最多包含 n^(n-2) 颗生成树。
- 如果在边中加上权值,那么权值最小的生成树即为最小生成树,权值最大的生成树为最大生成树。
最小生成树(带权连通图)、
所谓最小生成树,就是在一个具有N个顶点的带权连通图G中,如果存在某个子图G',其包含了图G中的所有顶点和一部分边,且不形成回路,并且子图G'的各边权值之和最小,则称G'为图G的最小生成树。
由定义我们可得知最小生成树的三个性质:
• 最小生成树不能有回路。
• 最小生成树可能是一个,也可能是多个。
• 最小生成树边的个数等于顶点的个数减一。
两种最小生成树的算法,分别为克鲁斯卡尔算法(Kruskal Algorithm)和普利姆算法(Prim Algorithm)。
克鲁斯卡尔算法(Kruskal Algorithm)、
参考视频 :超丝滑的最小生成树演示--克鲁斯卡尔算法!
克鲁斯卡尔算法的核心思想是:在带权连通图中,不断地在边集合中找到权值最小的边,如果该边满足得到最小生成树的条件,就将其构造,直到最后一条边得到一颗最小生成树。
克鲁斯卡尔算法的执行步骤:
- 第一步:在带权连通图中,将边的权值排序按小到大排序。
- 第二步:按权值从小到大依次取出边,并且判断是否需要选择这条边(此时图中的边已按权值从小到大排好序)。判断的依据是是否出现环路,如果不出现环路,那么就选择加入这条边,出现环路就抛弃掉。
- 第三步:循环第二步,直到图中所有的顶点都在同一个连通分量中,即得到最小生成树。
普利姆算法(Prim Algorithm)、
参考视频:【算法】最小生成树
普利姆算法的核心思想是:
- 一个加权连通图,其中顶点集合为V,边集合为E,初始化 Vnew = {x},其中x为集合V中的任一节点(起始点),Enew = {},为空。
- 重复下列操作,直到 Vnew = V。
- 在集合E中选取权值最小的边<u, v>,其中u为集合Vnew中的元素,而v不在Vnew集合当中,并且v∈V(如果存在有多条满足前述条件即具有相同权值的边,则可任意选取其中之一),将v加入集合Vnew中,将<u, v>边加入集合Enew中。
- 使用集合Vnew和Enew来描述所得到的最小生成树。
#include<iostream>
#include<cassert>
#include<algorithm>
#include<vector>
#include<queue>
using namespace std;
//格式化print函数
template<class...Args>
inline void print(const Args&... args) noexcept
{
((cout << args), ...);
}
//并查集
class Union_Find_Disjoint_Sets
{
public:
//并查集初始化操作,默认初始时所有的结点的根节点就是自身
Union_Find_Disjoint_Sets(size_t n)
{
_set.resize(n + 1, 0);
for (size_t i = 0; i < n + 1; ++i)
{
_set[i] = i;
}
}
~Union_Find_Disjoint_Sets()noexcept {}
//把两个结点i和j合并成为同一个结点
void merge(size_t i, size_t j)
{
size_t a = _find_root(i); //先找到i的根节点,得到根节点的编号
size_t b = _find_root(j); //然后在找到j的根节点,得到根节点的编号
_set[a] = b; //连接i和j
_set[i] = b; //路径压缩
}
//检测根节点i和j是不是在同一个关系中,也就是怕段它们是否有相同的根节点
bool test(size_t i, size_t j)
{
size_t a = _find_root(i);
size_t b = _find_root(j);
return a == b;
}
protected:
//找一个结点的根结点,得到根节点的编号
size_t _find_root(size_t x)
{
assert(x >= 0 && x < _set.size());
if (_set[x] == x) //这个情况是根节点就是自身
{
return _set[x];
}
return _set[x] = _find_root(_set[x]); //这个情况是根节点不是自身,那就继续递归,同时做一个路径压缩操作
}
private:
//并查集数组
vector<size_t> _set;
};
//边结构体
struct edge
{
edge(int b,int e,int w) : begin(b),end(e),weight(w) {}
int begin; //边的起始顶点
int end; //边的结束顶点
int weight; //权值
};
//顶点结构体
struct vertex
{
vertex(int n) : number(n),is_visited(false) {}
int number; //顶点编号
bool is_visited; //标志顶点是否被访问过
};
//图的邻接表存储结构
struct graph
{
vector<vertex*> V; //存储图的所有顶点
vector<edge*> E; //存储图的所有边
};
//两个仿函数用于权值大小比较
struct compare1
{
bool operator()(edge* l,edge* r) const
{
return l->weight < r->weight;
}
};
struct compare2
{
bool operator()(edge* l,edge* r) noexcept
{
return l->weight > r->weight;
}
};
//Prim algorithm
void Prim(graph& g) noexcept
{
vector<vertex*> v_new;
v_new.push_back(g.V[5]);
sort(g.E.begin(),g.E.end(),compare1());
vector<edge*> e_new;
while(v_new.size() != g.V.size())
{
for(auto i : g.E)
{
auto iter1 = find_if(v_new.begin(),v_new.end(),[&](auto x){return x->number == i->begin;});
auto iter2 = find_if(g.V.begin(),g.V.end(),[&](auto x){return x->number == i->end;});
auto iter3 = find_if(v_new.begin(),v_new.end(),[&](auto x){return x->number == i->end;});
if(iter1 != v_new.end() && iter2 != g.V.end() && iter3 == v_new.end())
{
e_new.push_back(i);
v_new.push_back(*iter2);
break;
}
//特别注意!!!
//由于无向图的一条边是没有方向的,一条边可以当作两条边!!!
//即起始顶点和结束顶点是相反的!!!
//这里要进行两次判断,不然会得不到正确答案!!!
//也可以在构造图的边时构造出两条结束顶点和起始顶点相反的边,这样这里就不需要判断两次了!!!
iter1 = find_if(v_new.begin(),v_new.end(),[&](auto x){return x->number == i->end;});
iter2 = find_if(g.V.begin(),g.V.end(),[&](auto x){return x->number == i->begin;});
iter3 = find_if(v_new.begin(),v_new.end(),[&](auto x){return x->number == i->begin;});
if(iter1 != v_new.end() && iter2 != g.V.end() && iter3 == v_new.end())
{
e_new.push_back(i);
v_new.push_back(*iter2);
break;
}
}
}
cout << "Prim algorithm :" << endl;
for(auto c: e_new)
{
print("边开始 : ",c->begin," 边结束 : ",c->end," 权值 : ",c->weight,"\n");
}
}
//Kruskal algorithm
void Kruskal(graph& g) noexcept
{
priority_queue<edge*,vector<edge*>,compare2> E;
for(auto c : g.E)
{
E.push(c);
}
vector<edge*> new_edge;
Union_Find_Disjoint_Sets set(g.V.size());
while(!E.empty())
{
auto tmp = E.top();
E.pop();
if(!set.test(tmp->begin,tmp->end))
{
set.merge(tmp->begin,tmp->end);
new_edge.push_back(tmp);
}
}
cout << "Kruskal algorithm :" << endl;
for(auto c : new_edge)
{
print("边开始 : ",c->begin," 边结束 : ",c->end," 权值 : ",c->weight,"\n");
}
}
int main()
{
graph g;
//构造顶点
for(int i = 1;i < 8;++i)
{
g.V.push_back(new vertex(i));
}
//构造边
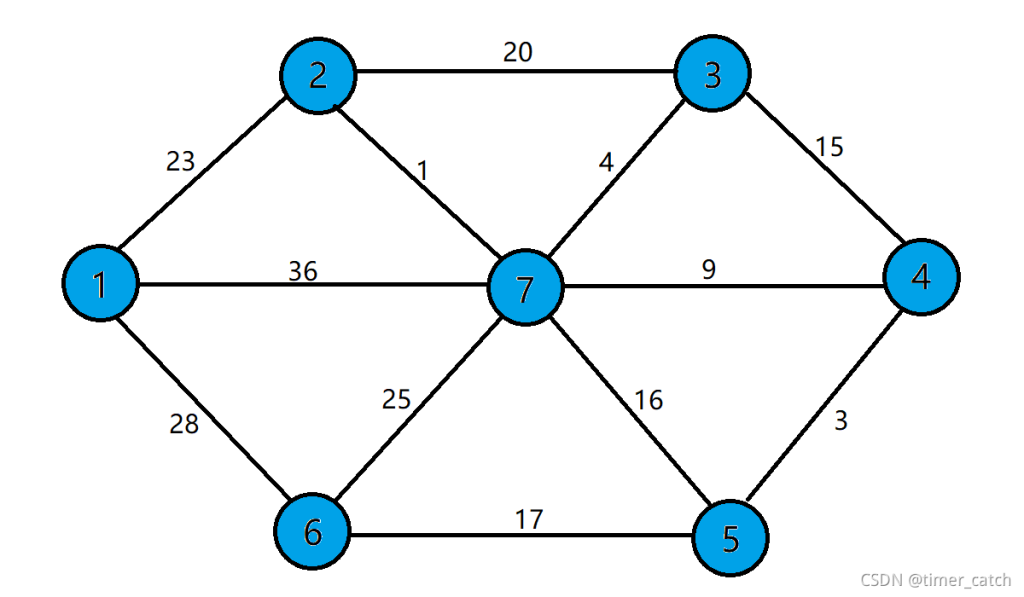
g.E.push_back(new edge(1,2,23));
g.E.push_back(new edge(1,7,36));
g.E.push_back(new edge(1,6,28));
g.E.push_back(new edge(2,7,1));
g.E.push_back(new edge(2,3,20));
g.E.push_back(new edge(3,7,4));
g.E.push_back(new edge(3,4,15));
g.E.push_back(new edge(4,7,9));
g.E.push_back(new edge(4,5,3));
g.E.push_back(new edge(5,7,16));
g.E.push_back(new edge(5,6,17));
g.E.push_back(new edge(6,7,25));
Prim(g);
cout << endl;
Kruskal(g);
//销毁所有顶点和边
for(auto c : g.V)
{
delete c;
}
for(auto c : g.E)
{
delete c;
}
return 0;
}

Comments NOTHING