数据结构并查集

定义、

并查集是一种树型的数据结构，用于处理一些不相交集合（disjoint sets）的合并及查询问题。

按照我自己的理解，我假设有n个树结点，并且这些树节点最开始时都是独立不相连的状态，例如下面这样。

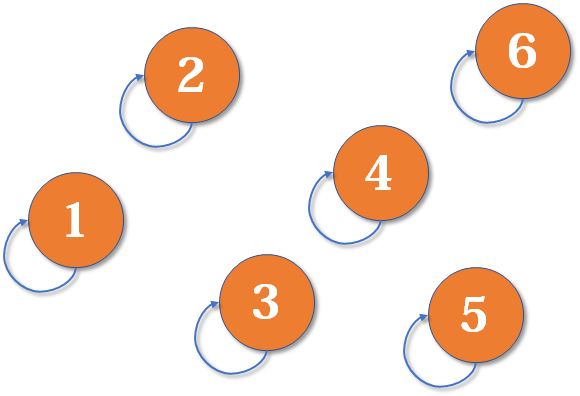
现在我要求结点1和结点3相连，如下所示。

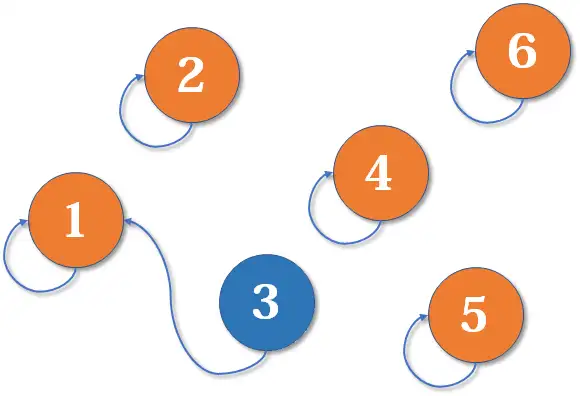
然后又让结点1和2相连。。。。。。

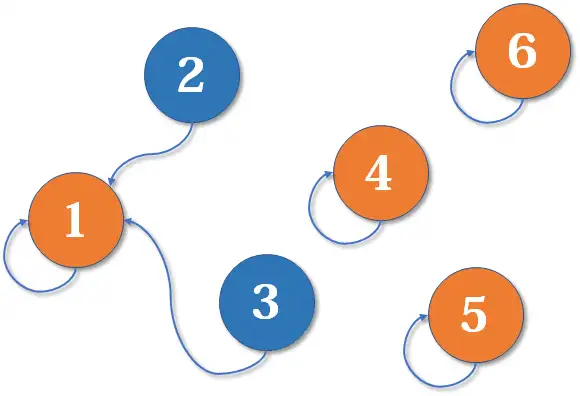
经过我的一系列要求后，最终变成下面这样。

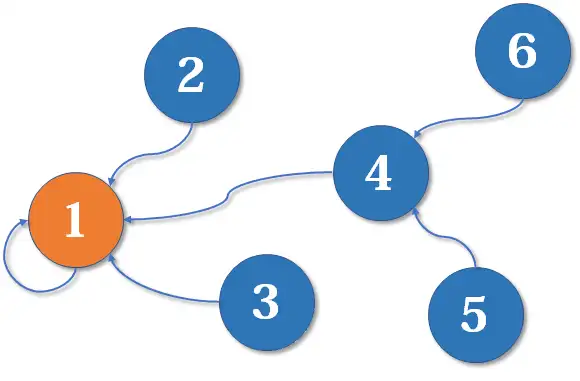
这就是明显的一个树，根节点为结点1，注意这是一个无向图。

我们用数组的下标来表示树节点的编号，用对应下标的值即根节点的编号来表示当前树节点的根节点。如果任意两个结点都有相同的根节点，那么就表示这两个结点是有关系的。

经典例题、

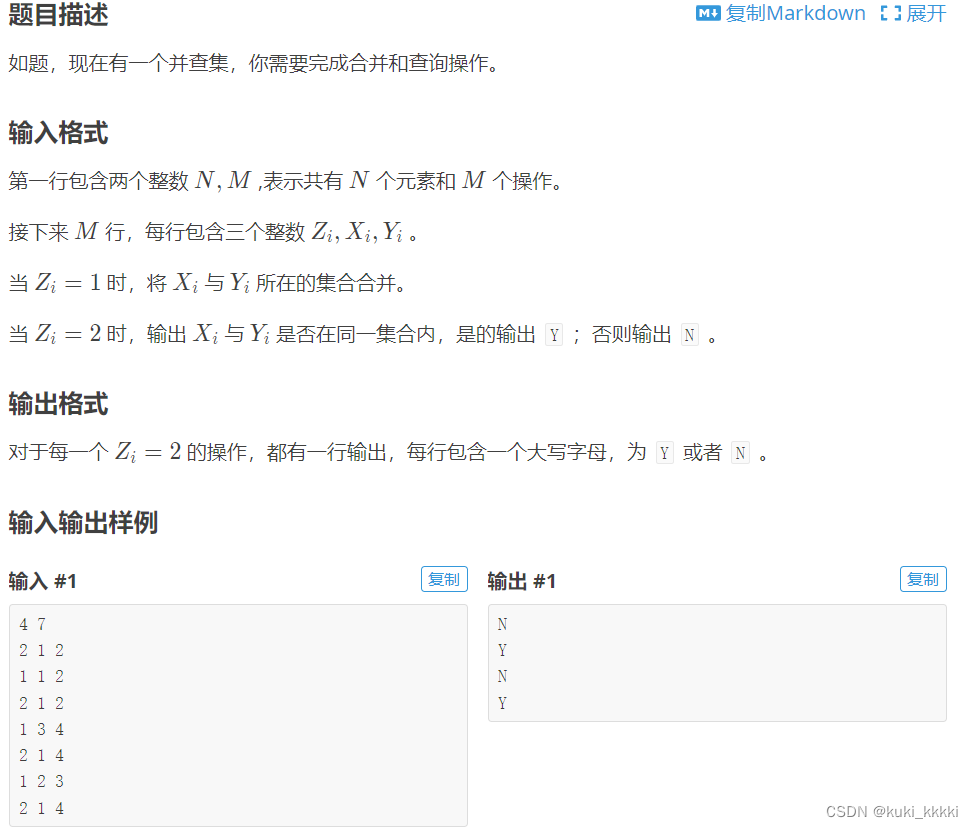
代码实现和解题

class Union_Find_Disjoint_Sets
{
public:

	//并查集初始化操作，默认初始时所有的结点的根节点就是自身
	Union_Find_Disjoint_Sets(size_t n)
	{
		_set.resize(n+1, 0);
		for (size_t i = 0; i <n+1; ++i)
		{
			_set[i] = i;
		}
	}


	~Union_Find_Disjoint_Sets()noexcept{}


	//把两个结点i和j合并成为同一个结点
	void merge(size_t i, size_t j)
	{
		size_t a = _find_root(i);    //先找到i的根节点，得到根节点的编号
		size_t b = _find_root(j);    //然后在找到j的根节点，得到根节点的编号
		_set[a] = b;                        //连接i和j
		_set[i] = b;                         //路径压缩
	}

	//检测根节点i和j是不是在同一个关系中，也就是怕段它们是否有相同的根节点
	bool test(size_t i, size_t j)
	{
		size_t a = _find_root(i);
		size_t b = _find_root(j);
		return a == b;
	}

protected:

	//找一个结点的根结点，得到根节点的编号
	size_t _find_root(size_t x)
	{
		assert(x >= 0 && x < _set.size());
		if (_set[x] == x)     //这个情况是根节点就是自身
		{
			return x;
		}
		return _set[x] = _find_root(_set[x]);   //这个情况是根节点不是自身，那就继续递归，同时做一个路径压缩操作
	}


private:
	
	//并查集数组
	vector<size_t> _set;
};


int main()
{

	int a{0}, b{ 0 }, c{ 0 }, d{ 0 }, e{ 0 };
	cin >> a >> b;
	Union_Find_Disjoint_Sets set(a);
	while (b--)
	{
		cin >> c;
		if (c == 1)
		{
			cin >> d >> e;
			set.merge(d, e);
		}
		else if (c == 2)
		{
			cin >> d >> e;
			if (set.test(d, e))
			{
				cout << "Y" << endl;
			}
			else
			{
				cout << "N" << endl;
			}
		}
	}
	return 0;
}