BF(暴力算法)、
正如其名字相同,该算法就是一个暴力求解的算法,不断遍历字符串每一个字符,如果该字符于匹配模式串的第一个字符相等,就进行匹配,如果在匹配的过程中发现有一个字符不匹配,就退出匹配,继续下一轮。时间复杂度是O(n*m),n,m分别代表两个字符串的长度,效率很低。
//暴力匹配
int64_t BF(const string& str, const string& pattern)
{
size_t s1 = str.size();
size_t s2 = pattern.size();
if (s1 < s2 || str.empty() || pattern.empty())
{
return -1;
}
size_t j = 0;
size_t i = 0;
for (; i < s1 && j < s2;)
{
if (str[i] == pattern[j])
{
++j;
++i;
}
else
{
i = i - j + 1;
j = 0;
}
}
return j >= s2 ? i - j : -1;
}
KMP算法、
有句话可以这么形容KMP:一个人能走的多远不在于他在顺境时能走的多快,而在于 他在逆境时多久能找到曾经的自己。KMP算法是一个字符串匹配算法,取得是三个发明人的名字首字母。
KMP算法一种改进的模式匹配算法,它的改进在于:每当从某个起始位置开始一趟比较后,在匹配过程中出现失配,不回溯,而是利用已经得到的部分匹配结果,将一种假想的位置定位“指针”在模式上 向右滑动尽可能远的一段距离到某个位置后,继续按规则进行下一次的比较。
KMP算法的时间复杂度是O(n),其中n是主串的长度。
KMP算法中一些重要的概念、
最长公共前后缀:前缀是指包含第一个字符的子串,后缀是指包含最后一个字符的子串。最长公共就是前缀和后缀要相等,且长度要为最长,但是这个长度不能等于字符串的长度,否则就没有意义了。
next数组:首先next数组是针对较小的字符串而言的,换句话说就是需要匹配的字符串。其次,该数组的每个位置的值(或者叫信息)其实是跟该位置没有关系,它其实表示的是它前一位置的信息,这个信息是什么呢?就是该位置的前一位置的最长公共前后缀的长度。
给定义一个字符串,如下所示:
string str = "AABCACD";
需要定义一个next数组来辅助KMP算法
int *next = new int[str.size()]{};
我们人为的规定,next[0]=-1,next[1]=0;
size_t i = 0;
next[i++] = -1; //i=0
next[i++] = 0; //i=1
next[i++] = 1; //i=2,表示pattern[i]之前的字符的最长公共前后缀,不包括pattern[i]
next[i++] = 0; //i=3
next[i++] = 0; //i=4
next[i++] = 1; //i=5
next[i++] = 0; //i=6
KMP完整实现、
// 计算next数组
int64_t* _get_next_(const string& pattern)
{
size_t size = pattern.size();
int64_t* next = new int64_t[size] {};
next[0] = -1; //人为规则为-1
next[1] = 0; //人为规则为0
size_t i = 2;
size_t cn = 0;
while (i < size)
{
if (pattern[i - 1] == pattern[cn])
{
next[i++] = ++cn;
}
else if (cn > 0)
{
cn = next[cn];
}
else
{
next[i++] = 0;
}
}
return next;
}
//KMP匹配,不适用于单个字符匹配!!!
int64_t KMP(const string& str, const string& pattern)
{
size_t s1 = str.size();
size_t s2 = pattern.size();
if (s1 < s2 || s2 == 1 || str.empty() || pattern.empty())
{
return -1;
}
int64_t* next = _get_next_(pattern);
if (!next)
{
return -1;
}
size_t i = 0; //指向str的首元素指针
size_t j = 0; //指向pattern的首元素指针
while (i < s1 && j < s2)
{
if (str[i] == pattern[j])
{
i++;
j++;
}
else if( j != 0)
{
j = next[j];
}
else
{
++i;
}
}
delete[]next;
next = nullptr;
return j == s2 ? i - j : -1;
}
测试、
#include<iostream>
using namespace std;
#define _CRTDBG_MAP_ALLOC
#include<crtdbg.h>
#include<cassert>
#include<algorithm>
#include<string>
#include<time.h>
void optimize_iostream_and_check_leak_memory()
{
_CrtSetDbgFlag(33);
std::ios::sync_with_stdio(false);
std::cin.tie(0);
std::cout.tie(0);
}
// 计算next数组
int64_t* _get_next_(const string& pattern)
{
size_t size = pattern.size();
int64_t* next = new int64_t[size] {};
next[0] = -1; //人为规则为-1
next[1] = 0; //人为规则为0
size_t i = 2;
size_t cn = 0;
while (i < size)
{
if (pattern[i - 1] == pattern[cn])
{
next[i++] = ++cn;
}
else if (cn > 0)
{
cn = next[cn];
}
else
{
next[i++] = 0;
}
}
return next;
}
//KMP匹配,不适用于单个字符匹配!!!
int64_t KMP(const string& str, const string& pattern)
{
size_t s1 = str.size();
size_t s2 = pattern.size();
if (s1 < s2 || s2 == 1 || str.empty() || pattern.empty())
{
return -1;
}
int64_t* next = _get_next_(pattern);
if (!next)
{
return -1;
}
size_t i = 0; //指向str的首元素指针
size_t j = 0; //指向pattern的首元素指针
while (i < s1 && j < s2)
{
if (str[i] == pattern[j])
{
i++;
j++;
}
else if( j != 0)
{
j = next[j];
}
else
{
++i;
}
}
delete[]next;
next = nullptr;
return j == s2 ? i - j : -1;
}
//暴力匹配
int64_t BF(const string& str, const string& pattern)
{
size_t s1 = str.size();
size_t s2 = pattern.size();
if (s1 < s2 || str.empty() || pattern.empty())
{
return -1;
}
size_t n = 0;
for (size_t i = 0; i <= s1 - s2; ++i)
{
n = 0;
if (str[i] == pattern[0])
{
for (size_t j = 1, k = i + 1; j < s2; ++j,++k)
{
if (str[k] != val[j])
{
break;
}
++n;
}
if (n == (s2 - 1))
{
return i;
}
}
}
return -1;
int64_t BF(const string& str, const string& pattern)
{
size_t s1 = str.size();
size_t s2 = pattern.size();
if (s1 < s2 || str.empty() || pattern.empty())
{
return -1;
}
size_t j = 0;
size_t i = 0;
for (; i < s1 && j < s2;)
{
if (str[i] == pattern[j])
{
++j;
++i;
}
else
{
i = i - j + 1;
j = 0;
}
}
return j >= s2 ? i - j : -1;
}
void Test()
{
string str{};
// 10000000 *26 个字符 a - z
for (size_t i = 0; i < 10000000; ++i)
{
for (char s = 'a'; s <= 'z'; ++s)
{
str.push_back(s);
}
}
string pattern = "abcdeffg"; //设置查找的字符在最后面,最坏的匹配情况
str += pattern;
auto begin = clock();
size_t pos = KMP(str, pattern);
auto end = clock();
cout << "KMP time = " << end - begin << endl;
cout << "pos = " << pos << endl;
auto begin2 = clock();
size_t pos2 = BF(str, pattern);
auto end2 = clock();
cout << "BF time = " << end2 - begin2 << endl;
cout << "pos = " << pos2 << endl;
auto begin3 = clock();
size_t pos3 = str.find(pattern);
auto end3 = clock();
cout << "Find time = " << end3 - begin3 << endl;
cout << "pos = " << pos3 << endl;
}
int main()
{
optimize_iostream_and_check_leak_memory();
Test();
return 0;
}
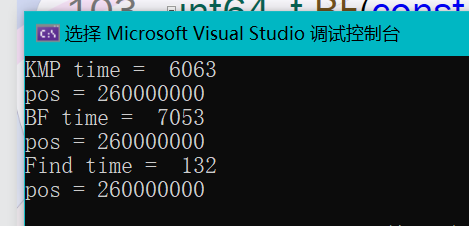
在我测试的情况下KMP和BF的差别不大,但与内置string的find方法就是一个天一个地了。
所以自己写的算法也就图一乐,使用时还得是用内置的算法。


Comments NOTHING