概念、
二叉搜索树虽可以缩短查找的效率O(logn),但如果数据有序或接近有序二叉搜索树将退化为单支树,查找元素相当于在顺序表中搜索元素,效率低下,时间复杂度是O(n)。因此,两位俄罗斯的数学家发明了一种解决上述问题的方法:当向二叉搜索树中插入新结点后,如果能保证每个结点的左右子树高度之差的绝对值不超过1(需要对树中的结点进行调整),即可降低树的高度,从而减少平均搜索长度,这就是AVL树。
AVL树节点设计、
class AVL_Tree_Node
{
public:
//这里省略了一些函数没写,比如拷贝构造,析构等等,但是不影响
AVL_Tree_Node(int data = 0):data(data){}
AVL_Tree_Node* left = nullptr; //左孩子节点指针
AVL_Tree_Node* right = nullptr; //右孩子节点指针
AVL_Tree_Node* parent = nullptr; //父节点指针
int data = 0; //data域
int64_t balance_value = 0; //平衡因子
};
旋转核心操作、
AVL树的核心在于任意一个节点,该节点的左右子树的高度差的绝对值小于2!!!定义平衡因子为左子树的高度减去右子树的高度,即该值必须小于2,大于等于2时就要进行旋转来保持平。下面就是两个核心的旋转!!!
(1)左旋转(RR型)
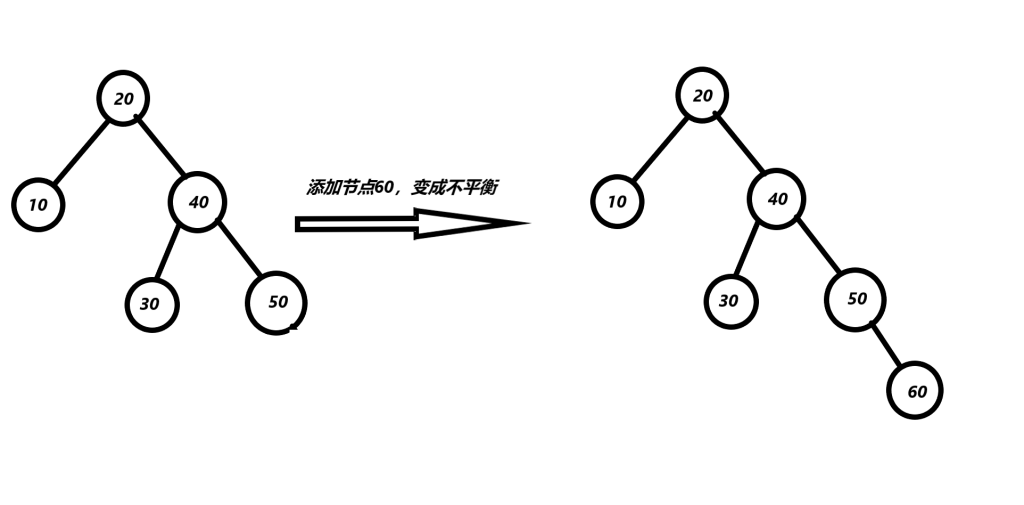
上图添加的节点是60节点,需要调整的是60节点至根节点中第一个不平衡的节点也就是节点20,因为20节点的平衡因子是 -2。
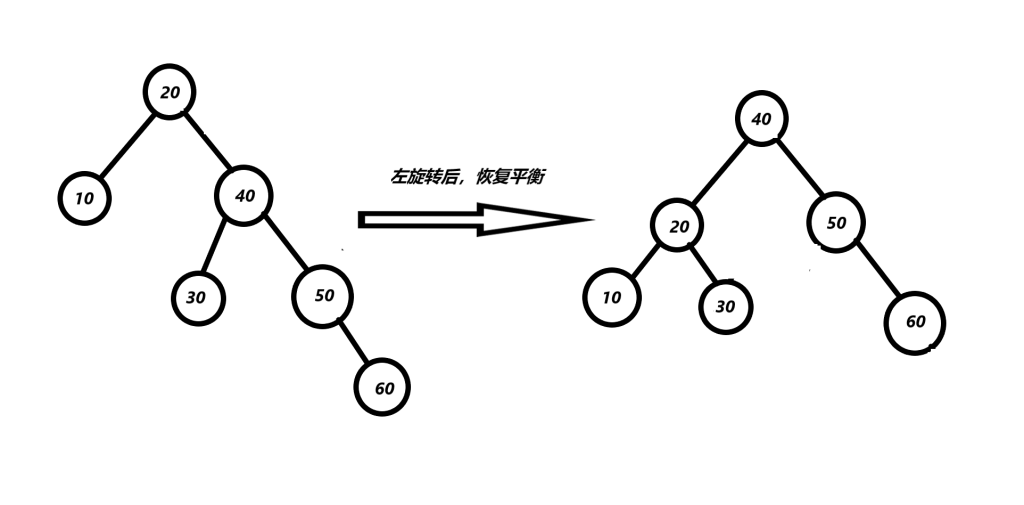
左旋的操作是使用两个指针,一个指针叫做parent指向不平衡的节点即节点20,另一个指针是cur指针,指向parent的右孩子即节点40。这两个指针的指向都是固定的。然后就开始调整指针的指向。
左旋转的条件为 :不平衡节点的平衡因子为-2,且右节点的平衡因子为-1,即 if (parent->balance_value == -2 && cur->balance_value == -1) 。
还有在更改指针指向时我们并不知道cur指向的节点有没有左子节点,parent有没有父节点,和parent是parent父节点的左子节点还是右子节点,都需要做判断!!!
//左旋,把parent结点作为右子节点的左子节点
void _rotate_left_(AVL_Tree_Node* parent)
{
AVL_Tree_Node* cur = parent->right; //parent的右子节点
AVL_Tree_Node* pp = parent->parent; //parent的父节点
AVL_Tree_Node* cur_left = cur->left; //cur的左节点
cur->left = parent; //更改指针指向
parent->parent = cur; //更改指针指向
parent->right = cur_left; //更改指针指向
if (cur_left) //判断cur有没有左子节点
{
cur_left->parent = parent;
}
if (pp) //有父节点,不是根节点的情况
{
if (pp->left == parent) //判断parent是父节点的左子节点还是右子节点
{
pp->left = cur;
}
else
{
pp->right = cur;
}
}
else //根节点的情况,需要更新根节点的信息
{
_root = cur;
}
cur->parent = pp;
//更新parent和cur的平衡因子信息
parent->balance_value = _height_(parent->left) - _height_(parent->right);
cur->balance_value = _height_(cur->left) - _height_(cur->right);
}
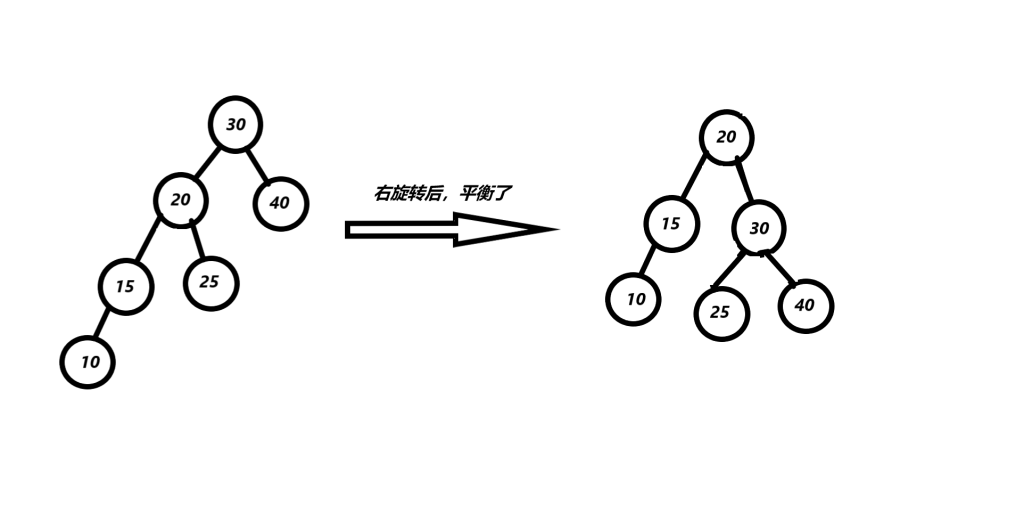
(2)右旋转(LL型)
右旋的逻辑和操作都和左旋差不多。

平衡破坏的节点是30,因为平衡因子为2。parent指针指向从插入节点10到根节点路径上第一个平衡破坏的节点也就是30,cur指针指向parent节点的左子节点,也就是20。然后开始调整指针。
右旋的条件为:if (parent->balance_value == 2 && cur->balance_value == 1)
还有在更改指针指向时我们并不知道cur指向的节点有没有左子节点,parent有没有父节点,和parent是parent父节点的左子节点还是右子节点,都需要做判断!!!
//右旋,把parent作为左子结点cur的右子结点
void _rotate_right_(AVL_Tree_Node* parent)
{
AVL_Tree_Node* cur = parent->left;
AVL_Tree_Node* pp = parent->parent;
AVL_Tree_Node* cur_right = cur->right;
cur->right = parent;
parent->parent = cur;
parent->left = cur_right;
if (cur_right)
{
cur_right->parent = parent;
}
if (pp)
{
if (pp->left == parent)
{
pp->left = cur;
}
else
{
pp->right = cur;
}
}
else
{
_root = cur;
}
cur->parent = pp;
parent->balance_value = _height_(parent->left) - _height_(parent->right);
cur->balance_value = _height_(cur->left) - _height_(cur->right);
}
(3)先左旋后右旋(LR型)
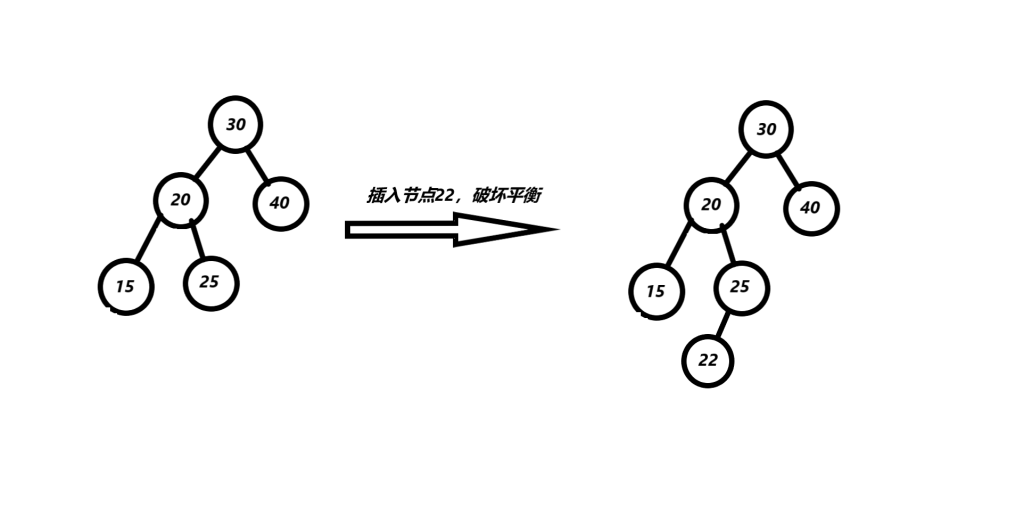
此时,破坏平衡的节点为30,平衡因子为2,parent指针指向30节点,cur指针指向30的左子节点20,20节点的平衡因子为-1。这种情况只旋转一次是不能平衡的,需要旋转两次。具体步骤是,先对cur指针左旋转,然后对parent指针右旋转。
旋转条件是: if (parent->balance_value == 2 && cur->balance_value == -1)

(4)先右旋后左旋(RL型)
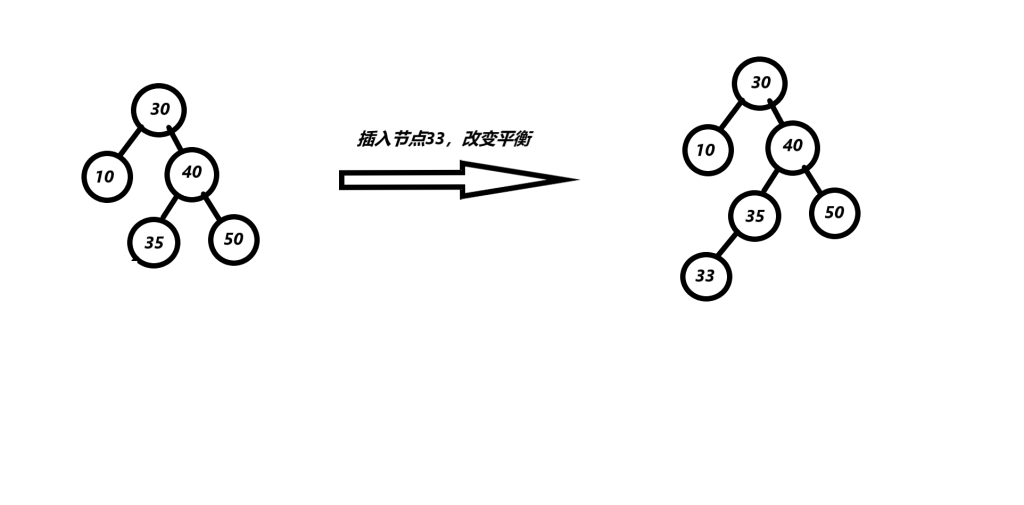
旋转条件是:if (parent->balance_value == -2 && cur->balance_value == 1)
parent指针指向节点30,cur指针指向节点40,然后分别对40节点进行右旋转,对30节点进行左旋转。
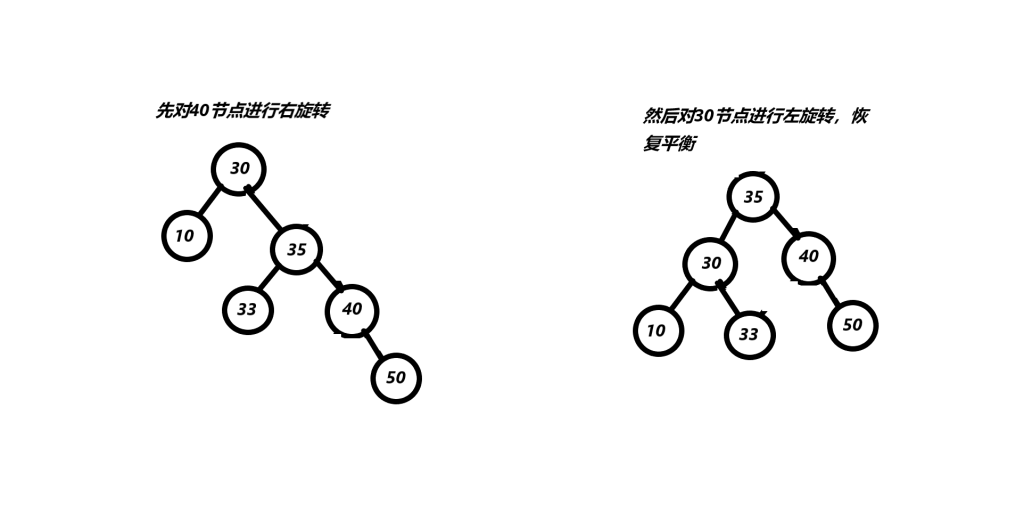
其实说白了双旋转就是左右旋转的组合而已,只要写好了最重要的左右旋转,双旋转完全没问题。我在写代码和测试代码的时候,出现了一个问题我弄了好久才解决,问题的原因在于旋转时少写了一个指针连接。。。折腾了我好久,所以写代码时一定要仔细和细心!!!
删除节点核心操作、
除了旋转操作,还有删除操作也是核心内容。
AVL 树的删除操作相对复杂一些,需要删除节点后回溯调整平衡到根节点。
AVL树删除一个节点,最坏情况下需要logn次旋转才能恢复平衡性质(需要回溯到根节点)。
AVL树的删除情况比较复杂,我现在还写不出没有bug的删除方法。。。。。。不过有一种取巧的方法,可以规避删除。具体是在树节点结构体中加入一个标识符来表示该节点是否存在,在使用树节点时要判断该标识符的真假,进而才能够使用节点。
AVL树的代码实现、
下面的代码删除操作存在bug,但是我现在看不出哪里有问题所以解决不了。。。其他操作没问题
class AVL_Tree_Node
{
public:
AVL_Tree_Node(int data = 0):data(data){}
AVL_Tree_Node* left = nullptr;
AVL_Tree_Node* right = nullptr;
AVL_Tree_Node* parent = nullptr;
int data = 0;
int64_t balance_value = 0;
};
class AVL_Tree
{
public:
AVL_Tree() :sizes(0), _root(nullptr) {}
~AVL_Tree()noexcept
{
clear();
}
//插入操作,没问题
void insert(int data)
{
//判断有没有根节点
if (_root == nullptr)
{
_root = new AVL_Tree_Node{ data };
++sizes;
return;
}
//判断是不是重复值
if (find(data) != nullptr)
{
return;
}
//寻找插入点
AVL_Tree_Node* pos = _root;
AVL_Tree_Node* parent = nullptr;
AVL_Tree_Node* new_node = new AVL_Tree_Node{ data };
while (pos)
{
parent = pos;
if (data > pos->data)
{
pos = pos->right;
}
else
{
pos = pos->left;
}
}
//插入
if (parent->data < data)
{
parent->right = new_node;
}
else
{
parent->left = new_node;
}
new_node->parent = parent;
++sizes;
//调平衡
_rotate_(parent, new_node);
}
//中序遍历
void in_order()const
{
_in_order_(_root);
}
//删除节点操作,有bug!!!具体在哪里我暂时看不出,目前解决不了
void remove(int data)
{
if (_root == nullptr || data==_root->data)
{
return;
}
stack<AVL_Tree_Node*>s{};
AVL_Tree_Node* pos = _root;
AVL_Tree_Node* parent = nullptr;
while (pos)
{
if (pos->data == data)
{
break;
}
parent = pos;
s.push(parent);
if (data > pos->data)
{
pos = pos->right;
}
else if (data < pos->data)
{
pos = pos->left;
}
}
if (pos == nullptr)
{
return;
}
if (!pos->left && !pos->right)
{
if (parent->left == pos)
{
parent->left = nullptr;
}
else
{
parent->right = nullptr;
}
delete pos;
--sizes;
parent->balance_value = _height_(parent->left) - _height_(parent->right);
}
else if (pos->left && pos->right)
{
AVL_Tree_Node* lmax = pos->left;
AVL_Tree_Node* lmax_parent = pos;
s.push(pos);
s.push(pos->right);
while (lmax->right)
{
lmax_parent = lmax;
s.push(lmax_parent);
lmax = lmax->right;
}
pos->data = lmax->data;
if (pos->left->right == nullptr)
{
lmax_parent->left = lmax->left;
}
else
{
lmax_parent->right = lmax->left;
}
if (lmax->left)
{
lmax->left->parent = lmax_parent;
}
delete lmax;
--sizes;
lmax_parent->balance_value = _height_(lmax_parent->left) - _height_(lmax_parent->right);
}
else if (pos->left && !pos->right)
{
if (parent->left == pos)
{
parent->left = pos->left;
}
else
{
parent->right = pos->left;
}
pos->left->parent = parent;
delete pos;
--sizes;
}
else if (pos->right && !pos->left)
{
if (parent->left == pos)
{
parent->left = pos->right;
}
else
{
parent->right = pos->right;
}
pos->right->parent = parent;
delete pos;
--sizes;
}
AVL_Tree_Node* cur = nullptr;
while (!s.empty())
{
cur = s.top();
s.pop();
_rotate_(cur->parent, cur);
}
}
//BFS
void BFS()
{
if (_root == nullptr)
{
return;
}
queue<AVL_Tree_Node*> q{};
q.push(_root);
AVL_Tree_Node* tmp = nullptr;
while (!q.empty())
{
tmp = q.front();
q.pop();
cout << "value = " << tmp->data << " balance value = " << tmp->balance_value << endl;
if (tmp->left)
{
q.push(tmp->left);
}
if (tmp->right)
{
q.push(tmp->right);
}
}
}
//DFS
void DFS()const
{
if (_root == nullptr)
{
return;
}
stack<AVL_Tree_Node*>s{};
s.push(_root);
AVL_Tree_Node* tmp = nullptr;
while (!s.empty())
{
tmp = s.top();
s.pop();
cout << tmp->data << " ";
if (tmp->left)
{
s.push(tmp->left);
}
if (tmp->right)
{
s.push(tmp->right);
}
}
}
//查找操作
AVL_Tree_Node* find(int data)const
{
AVL_Tree_Node* pos = _root;
while (pos)
{
if (data > pos->data)
{
pos = pos->right;
}
else if (data < pos->data)
{
pos = pos->left;
}
else
{
return pos;
}
}
return nullptr;
}
//树高度
int64_t height()const
{
return _height_(_root);
}
//清空操作
void clear()
{
_destroy_(_root);
sizes = 0;
_root = nullptr;
}
protected:
int64_t _height_(AVL_Tree_Node* _p)const
{
if (_p == nullptr)
{
return 0;
}
int64_t lh = 0, rh = 0;
lh = _height_(_p->left);
rh = _height_(_p->right);
return lh > rh ? ++lh : ++rh;
}
void _destroy_(AVL_Tree_Node* _p)
{
if (_p == nullptr)
{
return;
}
_destroy_(_p->left);
_destroy_(_p->right);
delete _p;
}
//右旋,把parent作为左子结点的右结点
void _rotate_right_(AVL_Tree_Node* parent)
{
//右旋转时并不知道cur有没有右结点,也不知道parent是parent的parent左节点还是右结点
//都需要进行判断
AVL_Tree_Node* cur = parent->left;
AVL_Tree_Node* pp = parent->parent;
AVL_Tree_Node* cur_right = cur->right;
cur->right = parent;
parent->parent = cur;
parent->left = cur_right;
if (cur_right)
{
cur_right->parent = parent;
}
if (pp)
{
if (pp->left == parent)
{
pp->left = cur;
}
else
{
pp->right = cur;
}
}
else
{
_root = cur;
}
cur->parent = pp;
parent->balance_value = _height_(parent->left) - _height_(parent->right);
cur->balance_value = _height_(cur->left) - _height_(cur->right);
}
//左旋,把parent结点作为右子结点的左子节点
void _rotate_left_(AVL_Tree_Node* parent)
{
AVL_Tree_Node* cur = parent->right; //右子节点
AVL_Tree_Node* pp = parent->parent;
AVL_Tree_Node* cur_left = cur->left; //右子节点的左节点
cur->left = parent;
parent->parent = cur;
parent->right = cur_left;
if (cur_left)
{
cur_left->parent = parent;
}
if (pp)
{
if (pp->left == parent)
{
pp->left = cur;
}
else
{
pp->right = cur;
}
}
else
{
_root = cur;
}
cur->parent = pp;
parent->balance_value = _height_(parent->left) - _height_(parent->right);
cur->balance_value = _height_(cur->left) - _height_(cur->right);
}
//中序遍历
void _in_order_(AVL_Tree_Node* _p)const
{
if (_p == nullptr)
{
return;
}
_in_order_(_p->left);
cout << _p->data << " ";
_in_order_(_p->right);
}
//旋转操作
void _rotate_(AVL_Tree_Node* parent, AVL_Tree_Node* cur)
{
while (parent && cur)
{
//更新节点平衡因子
parent->balance_value = _height_(parent->left) - _height_(parent->right);
//更新后的平衡因子为0的话,说明整棵树还是平衡的,直接退出
if (parent->balance_value == 0)
{
break;
}
//变成1或者-1的话说明有改变,继续循环下去
else if (parent->balance_value == 1 || parent->balance_value == -1)
{
cur = parent;
parent = parent->parent;
continue;
}
//右旋转
if (parent->balance_value == 2 && cur->balance_value == 1)
{
_rotate_right_(parent);
break;
}
//左旋,右边高度大于左边高度
else if (parent->balance_value == -2 && cur->balance_value == -1)
{
_rotate_left_(parent);
break;
}
//先左旋后右旋
else if (parent->balance_value == 2 && cur->balance_value == -1)
{
_rotate_left_(cur);
_rotate_right_(parent);
break;
}
//先右旋后左旋
else if (parent->balance_value == -2 && cur->balance_value == 1)
{
_rotate_right_(cur);
_rotate_left_(parent);
break;
}
}
//我发现的两个特殊情况,可能还有其他的特殊情况我目前没有发现
if (_root->balance_value == 2 && _root->right == nullptr)
{
_rotate_right_(_root);
}
else if (_root->balance_value == 2 && _root->left == nullptr)
{
_rotate_left_(_root);
}
}
private:
size_t sizes;
AVL_Tree_Node* _root;
};


Comments NOTHING