隐式空闲链表、
一个好的动态内存分配器,必须能解决之前提到的种种问题,比如如何记录空闲块?如何选择合适的空闲块并进行分配?当空闲块比申请空间大很多时,如何处理剩余部分?当一个已分配块被释放时,如何将它与周围的空闲块合并?
要解决这些问题,需要为每个块设计合理的数据结构,比如最简单的一种:隐式空闲链表,如下图所示:
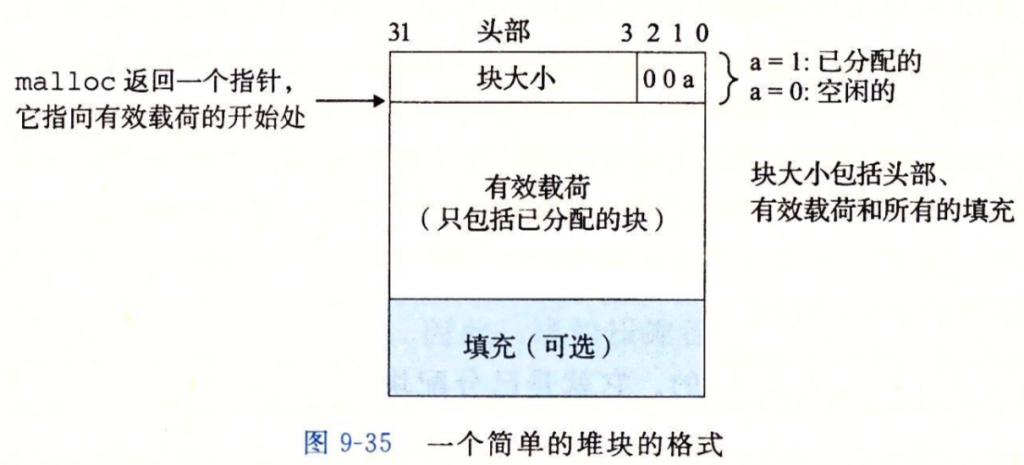
此时,一个块分三个部分,首先是一个8字节(字)的头部,头部会记录整个块(包括头部,有效载荷和填充)的大小,之所以用了8字节是因为我们这里采用了双字对齐要求,此外,由于双字对齐要求,所以整个块的大小一定是16字节的倍数,因此最低3位一定是0,为了更好地利用低3位,可以用它来标记当前块是已分配块还是空闲块,这里采用最低位作为已分配位。
当要响应申请内存的请求时,分配器会遍历此链表,找到大小合适的空闲块并进行分配,直到遍历到一个含有特殊标记的结束块,这里对结束块的定义是头部记录的块大小为0,且设置了已分配位的块。之所以称其为隐式空闲链表,是因为它里面没放指针,我们仅仅通过头部就可以知道这个块的大小,从而找到下一个块,这种数据结构的缺点是每次分配都要重新遍历链表,花费的时间与块的总数线性相关。
申请内存空间、
当我们申请内存空间时,分配器给我们的块大小一定是16个字节的倍数。且最低为需要设置为1来标识已分配。然后返回有效载荷的首地址指针。
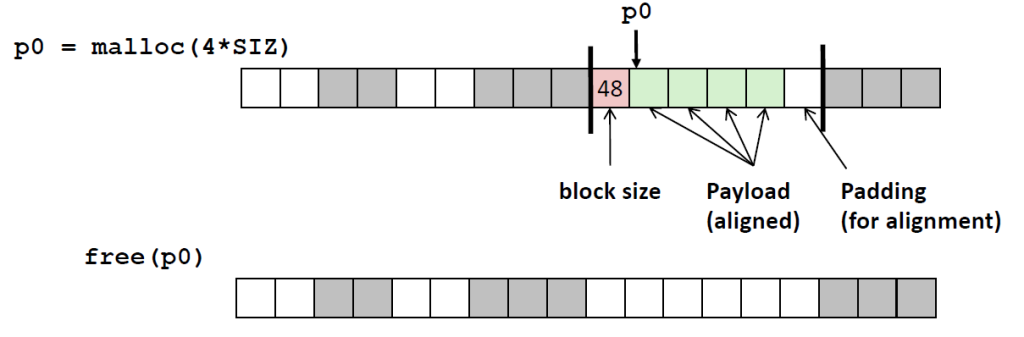
例如上述图中申请了4个block,在加上header总共5个block,由于对齐原则,实际上分配了6个block,共48个字节,最后一个block并没有使用,造成了碎片。通过下面的函数将分配标识位改为已分配。
void allocated(int& size)
{
size = size | 0x1;
// 0x1 : 00000000 00000000 00000000 00000001
//与0x1相或,只改变最低位为1,标记为已分配
}释放多少大小的内存空间、
我们要知道在释放时应该是释放多少空间,那么我们使用每一个块的header来得到释放的大小。
前面的word是这个block的header;后面的多余的空格即这个block的Padding(填充物)

但是实际上header存储的不是48,应该是 48 | 0x1,因为要标记为已分配。我们要通过变换才能得到真正的分配的字节数。
int size(int header)
{
return header & -2;
//与 -2 :11111111 11111111 11111111 11111110 相与
//只改变最低位,最低位变为0,效果为header-1
}Keeping Track of Free Blocks(追踪空闲的块)、
对于隐式的链表来说:
我们知道,每一个payload开始的位置必须是偶数个word,但是上面说了,每一个block的第一个word记录了这个block的大小。因此在堆的一开始我们必须空出来一个word。下面只介绍这一种方法,当然还有其他的方法。
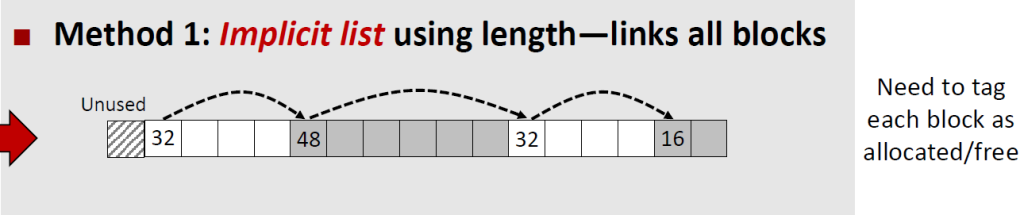
将一个block放大,我们可以看到这样的结构:
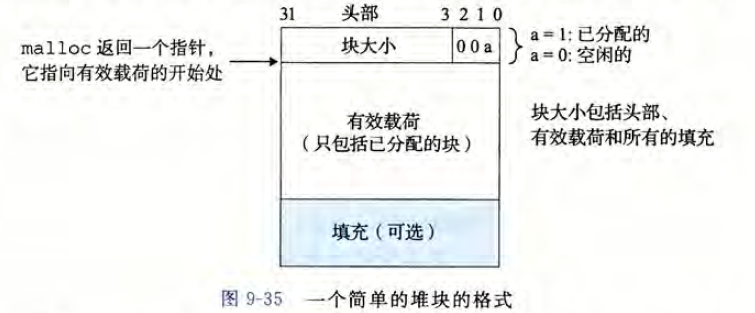
我们可以根据每一个header的存储的size大小,可以得到下一个header的地址。
验证一个块是不是已经分配过:
//分配过的结果是1,没有分配过的结果是0
bool is_allocated(int header)
{
return header & 0x1;
}更改最低分配位,释放块,需要合并相邻的块
void free_block(ptr p )
{
*p = *p & -2;
next = p + *p;
if((*next & 1) == 0)
{
*p = *p + *next;
}
}从隐式链表头部开始找到第一个空闲的block
p = start;
while((p < end) && (*p & 0x1) || (*p < len))
{
p = p + (*p & -2);
}
假设块的格式如上图所示,我们可以将堆组织为一个连续的已分配块和空闲块的序列
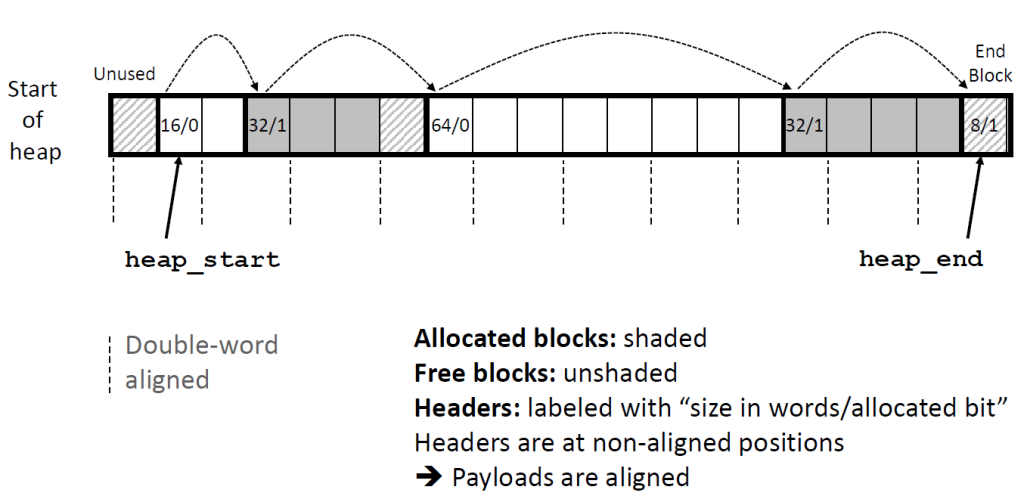
我们称这种结构为隐式空闲链表,是因为空闲块是通过头部中的大小字段隐含地连接着的。分配器可以通过遍历堆中所有的块,从而间接地遍历整个空闲块的集合。
注意,我们需要某种特殊标记的结束块,在这个示例中,就是一个设置了已分配位而大小为零的终止头部(end block)
隐式空闲链表的优点是简单。显著的缺点是任何操作的开销,例如放置分配的块,要求对空闲链表进行搜索,该搜索所需时间与堆中已分配块和空闲块的总数呈线性关系。
很重要的一点就是意识到系统对齐要求和分配器对块格式的选择会对分配器上的最小块大小有强制的要求。没有已分配块或者空闲块可以比这个最小值还小。例如,如果我们假设一个双字的对齐要求,那么每个块的大小都必须是双字(16字节)的倍数。因此,9-35的块格式就导致最小的块大小为两个字:一个字作头,另一个字维持对齐要求。即使应用只请求一字节,分配器也仍然需要创建一个两字的块。
放置策略(placement policy)、
当一个应用请求一个k字节的块的时候,分配器就会搜索空闲列表来查找一个足够大的可以放置所请求块的空闲块。我们有很多种放置策略:
首次适配
首次适配即从链表头开始查找,选择第一个合适的空闲块。
优点就是它趋向于将大的空闲块保留在链表后面
缺点是它趋向于在靠近链表起始处留下小空闲块的“碎片”,这就增加了对较大块的搜索时间
下一次适配和首次适配相似,只不过不是从链表的起始处开始搜索,而是从上一次查询结束的地方开始
下一次适配比首次适配运行起来明显要快一些。但是内存利用率要比首次适配低得多。
最佳适配是检査每个空闲块,选择适合所需请求大小的最小空闲块
最佳适配比首次是配合下一次适配的利用率都要高一点,但在简单空闲链表组织结构(如隐式空闲链表)当中,使用最佳适配的缺点就是它要求对堆进行彻底的搜索。
分割空闲块、
当我们找到一个匹配的空闲块之后,我们就需要分配这个空闲块中的空间。
我们自然可以选用整个空闲块,但是这样就会造成很多内部碎片。但如果放置策略趋向于产生较好的匹配,那么额外的内部碎片也是可以接受的。
但是如果匹配得不太好,那么分配器就通常会选择将这个空闲块分割为两部分。第一部分变成分配块,剩下的空间形成一个新的空闲块。
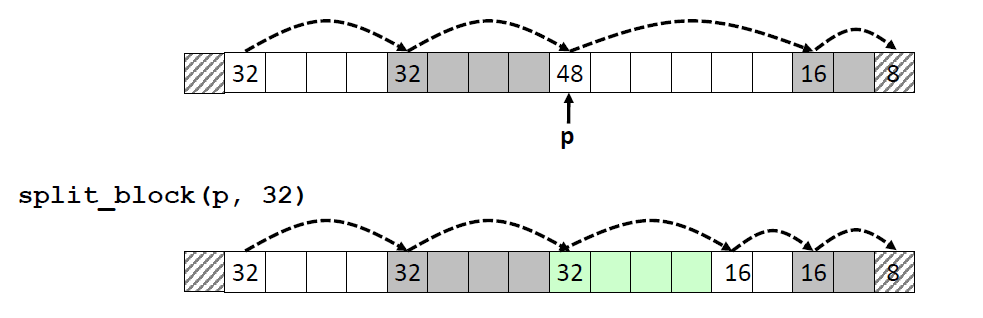
比如说上图,我们在size = 48的空闲块中插入一个size = 32的block,这时候空间块就会被拆成一个长为32的分配块、一个长为16的空闲块
释放、合并空闲块、
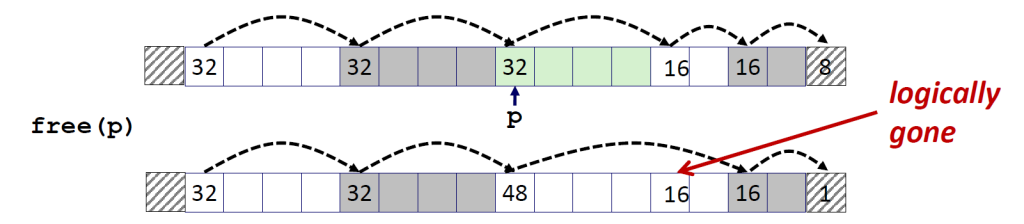
在释放块时,我们不需要对被释放的块的header进行修改。我们只需要跳过这个block,将前一个header指向下下个block的header即可。
上面所说的是和后面的block相连,但是如果想要和前一个block相连,那么事情就变得复杂起来了。因为如果我们的模型只是一个带头部的隐式空闲链表,就没有一个指针指向前面一个block。那么我们只能是搜索整个链表,同时记住前面块的位置。那么如果这样操作,我们会发现每次调用free所需要的时间都和堆的大小成线性关系。即使使用更复杂更精细的空闲链表,搜索时间也不会是常数。
带边界标记的合并、
于是我们可以将刚才提出的模型进行一个修改。这个修改是knuth提出来的。对于一个free block(空闲的块),我们可以把这个块的结尾处改成一个footer。其中,footer是header的一个副本。这个设计十分巧妙,如果每个块都包括这样一个footer,那么分配器就可以通过检查它的footer,来判断前面一个块的起始位置和状态。

那么当分配器释放当前块的时候,可能存在有以下四种情况
1) 前面的块和后面的块都是已分配的
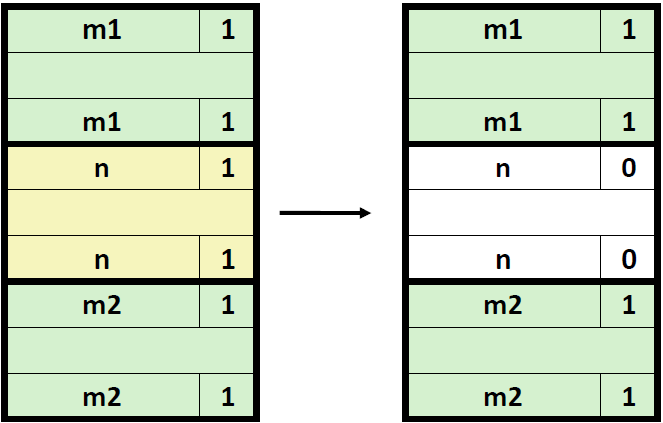
对于这种情况,我们只要将中间这个空闲块的header和footer的占用位从1改成0即可。
2) 前面的块是已分配的,后面的块是空闲的
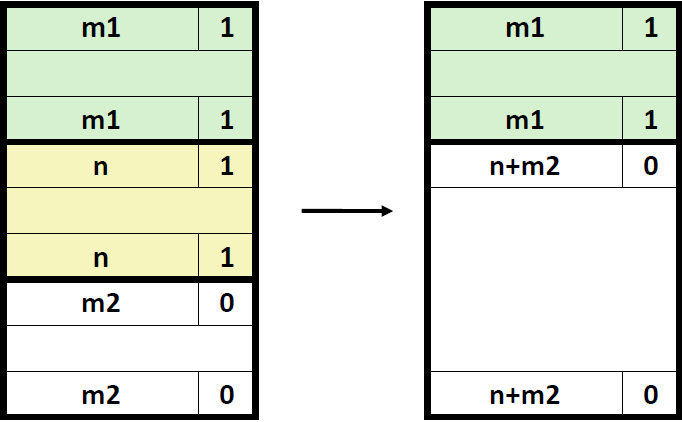
对于这种情况,新的header的和就等于释放的这一块的header+它后面那块free block的header,然后对footer也进行相应的修改。并将二者的占用位改成0
3) 前面的块是空闲的,后面的块是已分配的
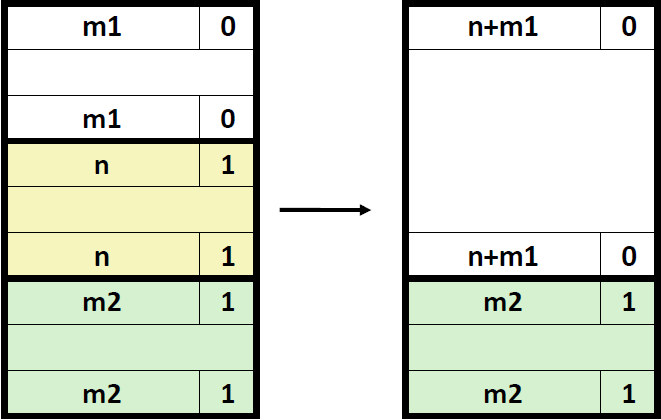
这种情况和2一样。
4) 前面的和后面的块都是空闲的
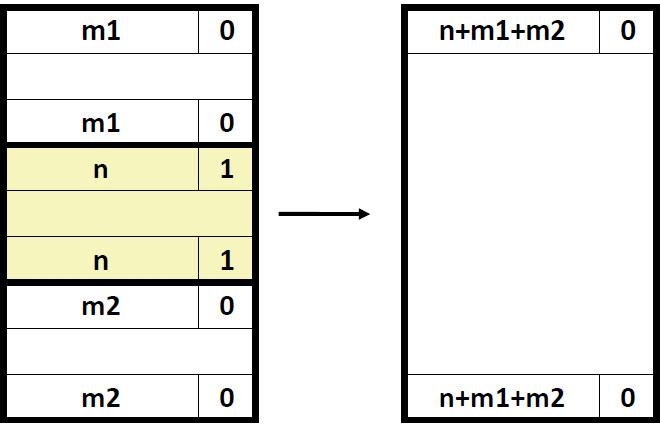
对于前面的块和后面的块都是free block的情况,我们需要修改前面的块的header和后面的块的footer。其大小就是将三个块的大小相加。对于中间这些数据,都被跳过了,不用去修改它们。
于是整个模型如下图所示:

我们发现最前面和最后面的两块空间是利用不起来的。因为malloc返回的地址并不是header的起始地址,而是payload的起始地址。而payload的起始地址必须是偶数对齐的,因此必须要有一个word空出来的。
因为heap是自底向上生长的,因此我们定义Dummy footer是在第一个block之前的;Dummy header是在最后一个block之后的。而且他们都要被标记成已分配,这是因为他们不能和block进行合并操作。
No Boundary Tag for Allocated Blocks(不带边界标记的合并)、
对于已经分配了的blocks来说,如果要有footer,由于对齐的原因,有可能要多两个字节来存放。因此,我们可以对分配了的block进行一些修改:
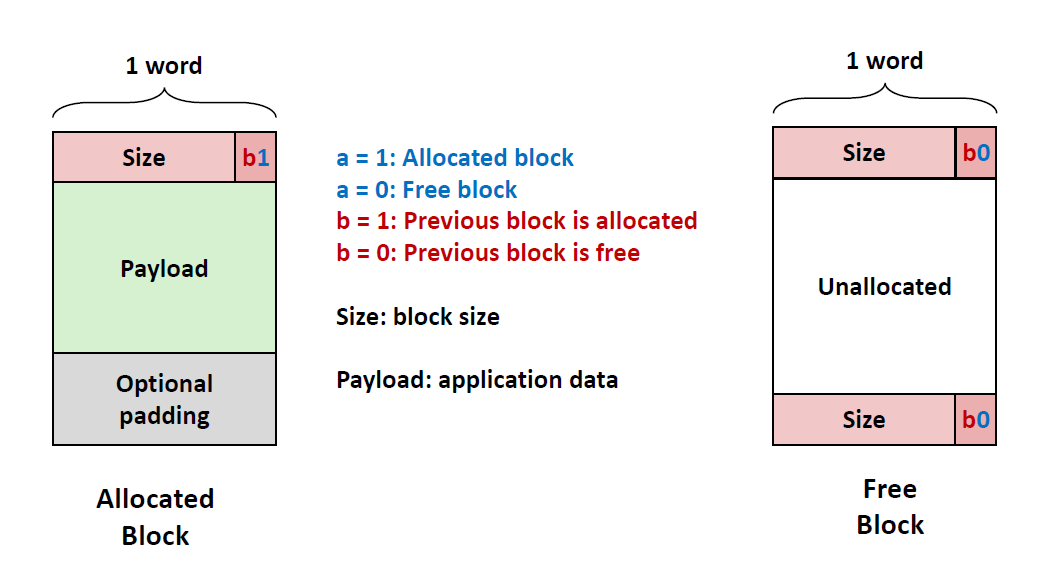
我们可以进一步地用2位来表示状态,多出来的一位可以用来表示前一个block是满的还是空的。这样,我们仅仅用一位就能节省额外地footer,分配了的block仅保留一个header。但是对于payload为空的块,我们还是保留footer。
那么上面所说的4种情况就要发生一些细小的改变了:
1) 前面的块和后面的块都是已分配的
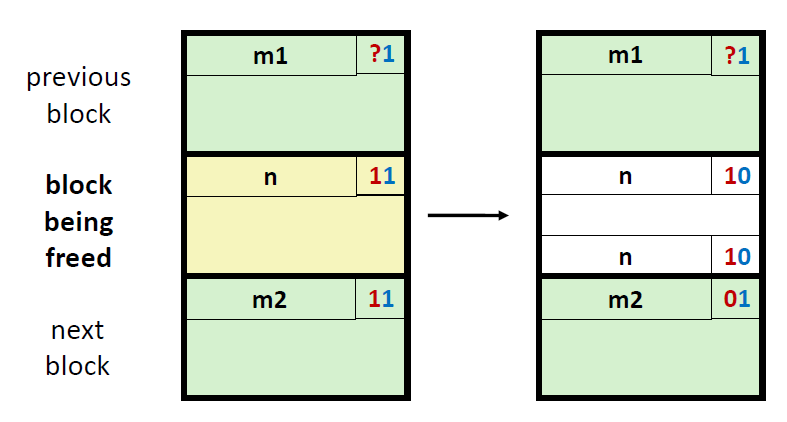
2) 前面的块是已分配的,后面的块是空闲的
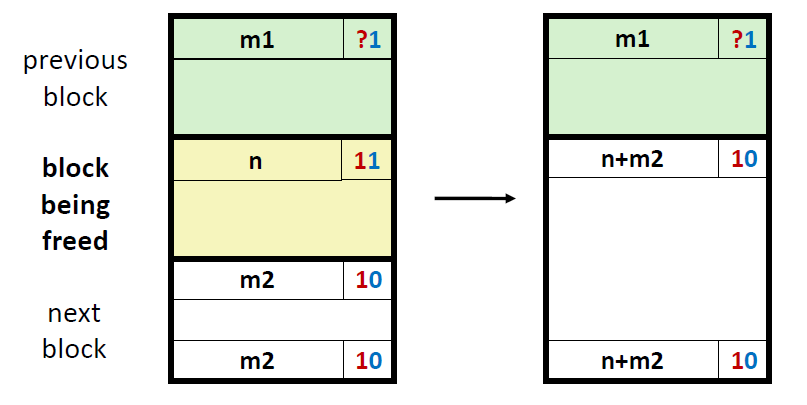
3) 前面的块是空闲的,后面的块是已分配的
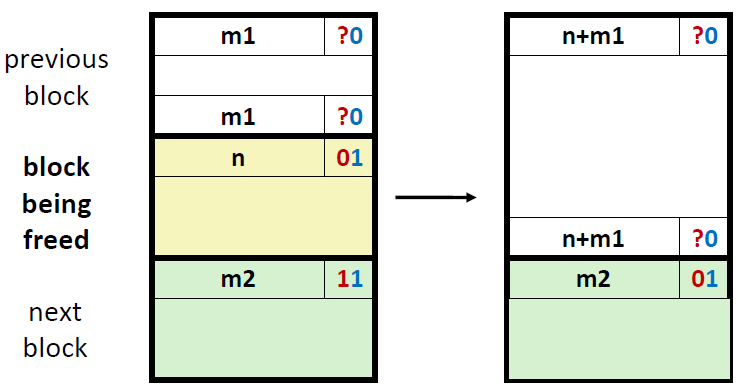
4) 前面的和后面的块都是空闲的
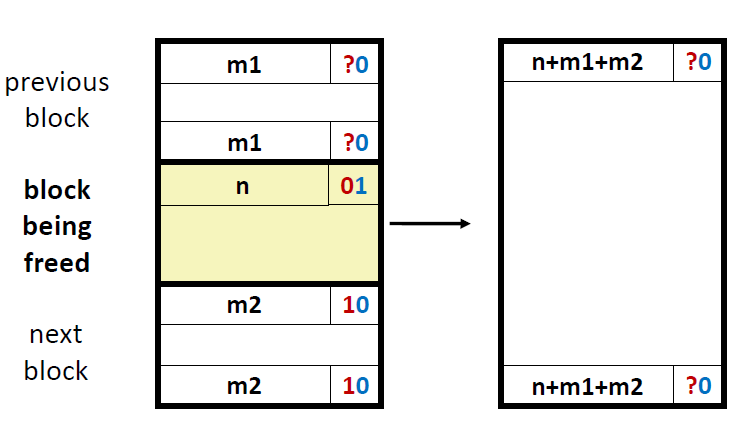


Comments NOTHING