路由选择算法,其目的是从发送方到接收方的过程中确定一条通过路由器网络的好的路径。通常,一条好路径指具有最低开销的路径。
可以用图来形式化描述路由问题。我们知道图(graph)G = (N,E)是一个N个节点和E条边的集合,其中每条边是取自N的一对节点。在网络层路由选择的环境中,图中的节点表示路由器,这是做出分组转发决定的点;连接这些节点的边表示这些路由器之间的物理链路。
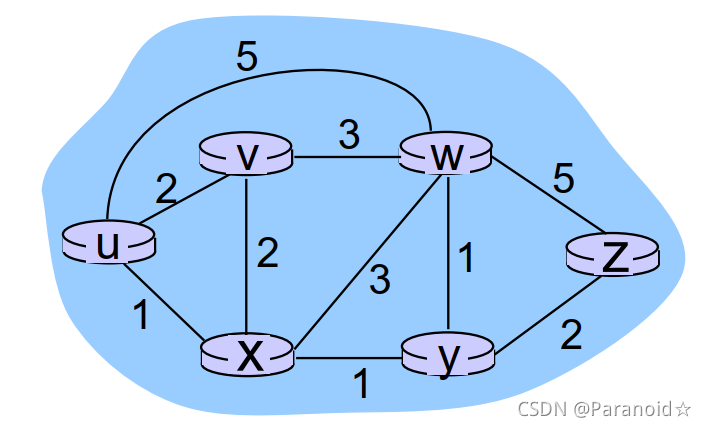
在图抽象中为各条边指派了开销后,路由选择算法的目标自然是找出从源到目的地间的最低开销路径。最短路径是在源和目的地之间的具有最少链路数量的路径。
一般而言,路由选择算法是一种分类方式是根据该算法是集中式还是分散式来划分的。
1)集中式路由选择算法用完整的、全局性的网络知识计算出从源到目的地之间的最低开销路径。也就是说,该算法以所有节点之间的连通性及所有链路的开销为输入。这就要求该算法在真正开始计算之前,要以某种方式获得这些信息。计算本身可在某个场点进行,或在每台路由器的路由选择组件中重复进行。然而,这里的主要区别在于,集中式算法具有关于连通性和链路开销方面的完整信息。具有全局状态信息的算法常被称为链路状态算法(Link State,LS),因为该算法必须知道网络中每条链路的开销。
2)分散式路由选择算法。路由器以迭代、分布式的方式计算出最低开销路径。没有节点拥有关于所有网络链路开销的完整信息。相反,每个节点仅有与其直接相连链路的开销知识即可开始工作。然后,通过迭代计算过程以及与相邻节点的信息交换,一个节点逐渐计算出到达某目的节点或一组目的节点的最低开销路径。我们将学习一个叫距离向量(distance-vector,DV)路由选择算法。每个节点维护到网络中所有其他节点的开销估计的向量。这种分散式算法,通过相邻路由器之间的交互式报文,也许更为天然的适合那些路由器直接交互的控制平面。
路由选择算法的第二种广义分类是根据算法是静态的还是动态的进行分类。在静态路由算法中(static routing algorithm)中,路由随时间的变化非常缓慢,通常是由人工进行调整,如增加一条路由。动态路由算法(dynamic routing algorithm)随着网络流量负载或拓扑发生变化而改变路由选择路径。一个动态算法可以周期性的运行或直接影响拓扑或链路开销的变化而运行。虽然动态算法易于对网络的变化而做出反应,但也更容易受诸如路由选择循环,路由振荡之类问题的影响。
链路状态路由算法(LS)、
在LS算法中,网络拓扑和所有链路的开销都是已知的,可以作为LS算法的输入。实践中这是通过让每个节点向网络中所有其他节点广播链路状态分组来完成的,其中每个链路状态分组包含她所连接的链路的标识和开销。由链路状态广播算法(Link state broadcast)来完成。节点广播的结果是所有节点都具有该网络的统一完整的视图。于是每个节点都能够像其他节点一样运行LS算法并计算出相同的最低开销路径集合。
下面学习的链路状态路由选择算法叫做Dijkstra算法,一种用于求解单源最短路径问题的算法,也就是说,它能够求出一个节点到其他所有接点的最短路径,但是它不能用于求出多源最短路径问题,即求出多个节点之间的最短路径。
当LS算法终止时,对于每个节点,我们都得到从源节点沿着它的最低开销路径的前一个节点。链路状态路由算法的主要优点是,每个路由结点都使用同样的原始状态数据独立地计算路径,而不依赖中间结点的计算;链路状态报文不加改变地传播,因此采用该算法易于查找故障。当一个结点从所有其他结点接收到报文时,它可以在本地立即计算正确的通路,保证一步汇聚。最后,由于链路状态报文仅运载来自单个结点关于直接链路的信息,其大小与网络中的路径结点数目无关,因此链路状态算法比距离-向量算法有更好的规模可伸展性。
OSPF(Open Shortest Path First开放式最短路径优先)是对链路状态路由协议的一种实现,著名的迪克斯加算法被用来计算最短路径树。OSPF支持负载均衡和基于服务类型的选路,也支持多种路由形式,如特定主机路由和子网路由等。OSPF的简单说就是两个相邻的路由器通过发报文的形式成为邻居关系,邻居再相互发送链路状态信息形成邻接关系,之后各自根据最短路径算法算出路由,放在OSPF路由表,OSPF路由与其他路由比较后优的加入全局路由表。
距离向量路由选择算法(DV 算法)、
相比于 LS 算法需要有网络的全局信息,DV 算法是一种迭代、异步和分布式的算法。分布式体现于算法的流程,是要每个节点都从一个或多个直接连接的邻居接收信息,通过对信息的计算,再把结果通告给邻居。迭代体现于算法对于上述的过程,需要一直持续到邻居之间没有信息需要交换位置。异步体现于不需要所有的节点统一进行操作,而是当收到邻居发来的信息进行操作即可。
DV 算法的原理使用了 Bellman-Ford 方程,具体内容如下。结合我们的情景讲一下每个参数,“c(x,v)” 表示 x 到邻居 v 的开销,dv(y) 表示从邻居 v 到目的地 y 的开销,我们需要在 x 的所有邻居中获得最小值。
dx(y) = minv{c(x,v) + dv(y)}
Bellman-Ford 方程为 DV 算法的与邻居的通信提供了理论基础。简单地说,也就是节点获得最短路径的下一跳,并且将该信息写入转发表中。这时我们也给出距离向量的定义,向量所表示的信息是 x 在 N 中到其他所有结点 y 的开销估计向量。
Dx = [Dy: y ∈ N]
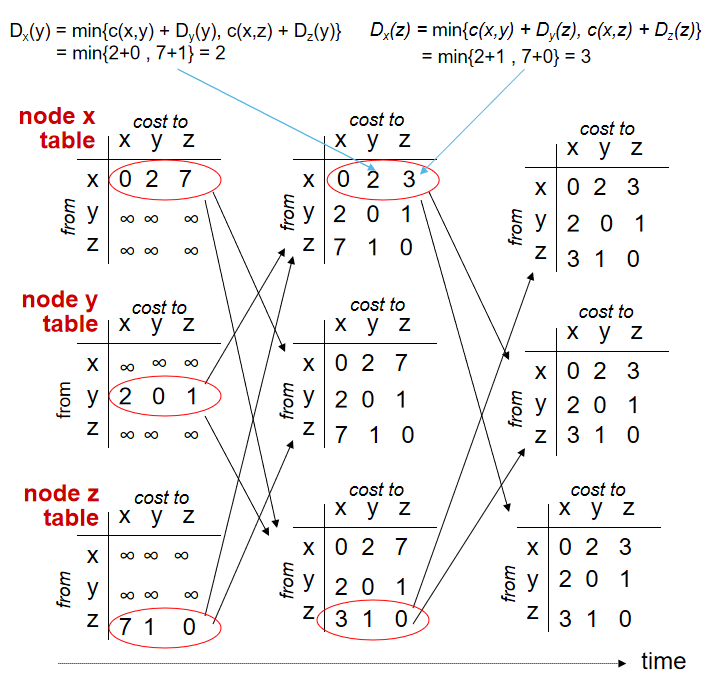
DV 算法对于一个节点 x 来说,当 x 发现与它直接连接的链路开销发生变化或从邻居接收到一个距离向量的更新时,重新计算距离向量的估计值,若最低开销路径发生了变化,就向邻居发送新的距离向量。具体怎么实现,通过一个例子来说明:

我们有一个简单的网络拓扑,有 v,y,z 3 个节点,下图中最左边就是 3 个节点的初始路由表。如图展示的就是根据 DV 算法更新路由表的过程。
LS 算法 VS DV 算法、
2 种算法采取不同的思路来得出最短路径,这 2 种算法在以下 3 个方面有着很明显的不同。
LS 算法需要知道网络中所有链路的开销,这就需要发送足够多的(O(|N||E|))报文才能获取,当任何一条链路开销发生改变时,也必须向所有的节点发送新的开销信息。而 DV 算法在每次迭代时,只需要 2 个直接相连的邻居交换报文即可。
LS 算法的时间复杂度和我们熟悉的 Dijkstra 算法相同,但是会遇到振荡问题,而 DV 算法也会遇到麻烦的无穷计数问题。
若网络中突然出现某台路由器故障、系统错乱或被蓄意破坏的情况。对于 LS 算法由于路由的计算时分离的,因此路由器可以向其连接的链路广播异常状态。对于 DV 算法来说,当产生了不正确的最低开销的计算结果,这个错误将会蔓延到整个网络。


Comments NOTHING