迪杰斯特拉算法是一种用于求解带权有向图中单源最短路径的算法。它以一个起始节点为基准,逐步扩展到其他节点,通过不断更新节点的最短路径来找到起始节点到其他节点的最短路径。
Diikstra算法的实现通常使用优先队列。算法过程:
- 1.创建一个空的优先队列Q,将起点加入Q中并设置起点到自身的距离为0,Q中优先级是起点到Q中每一点的距离越短越优先!!!
- 2.创建一个数组dist,用于保存起点到各个节点的距离,初始化为无穷大;
- 3.创建一个数组visited,用于标记节点是否被访问过,初始化为false;
- 4.将dist[起点]的值设置为0;
- 5.当Q不为空时,重复以下步骤;
- a.从Q中取出距离起点最近的节点i;
- b.如果节点i已经被访问过,则跳过此次循环;
- 如果节点i没有被访问过,则标记为已访问,对于i的每一个邻居节点j,如果i到j有路径且j没有被访问过且i到j的距离小于dist[j],则更新dist[j]的值为dist[j] = min((i到j的距离) + dist[i],dist[j]),然后把节点j加入到Q中;
#include<iostream>
#include<vector>
#include<queue>
#include<algorithm>
#include<climits>
using namespace std;
//初始化一个图
const size_t n = 7;
int graph[n][n];
void init() noexcept
{
for(size_t i = 0;i < n;++i)
{
for(size_t j = 0;j < n;++j)
{
graph[i][j] = -1;
if(i == j)
{
graph[i][j] = 0;
}
}
}
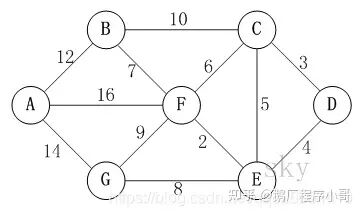
//A0,B1,C2,D3,E4,F5,G6
graph[0][1] = 12;
graph[0][5] = 16;
graph[0][6] = 14;
graph[1][0] = 12;
graph[1][5] = 7;
graph[1][2] = 10;
graph[2][1] = 10;
graph[2][5] = 6;
graph[2][4] = 5;
graph[2][3] = 3;
graph[3][2] = 3;
graph[3][4] = 4;
graph[4][3] = 4;
graph[4][2] = 5;
graph[4][5] = 2;
graph[4][6] = 8;
graph[5][2] = 6;
graph[5][4] = 2;
graph[5][6] = 9;
graph[5][0] = 16;
graph[5][1] = 7;
graph[6][0] = 14;
graph[6][4] = 8;
graph[6][5] = 9;
}
//一个辅助结构体
struct T
{
T(int a,int b) noexcept: v(a),d(b) {}
T() noexcept : v(0),d(0){}
T(const T& rhs) noexcept: v(rhs.v),d(rhs.d) {}
~T() noexcept {}
T& operator= (const T& rhs) noexcept
{
if(this != &rhs)
{
v = rhs.v;
d = rhs.d;
}
return *this;
}
friend bool operator <(const T& lhs,const T& rhs) noexcept
{
return lhs.d < rhs.d;
}
friend bool operator >(const T& lhs,const T& rhs) noexcept
{
return lhs.d > rhs.d;
}
friend bool operator ==(const T& lhs,const T& rhs) noexcept
{
return lhs.d == rhs.d && lhs.v == rhs.v;
}
int v; //节点编号
int d; //节点距离起点的距离
};
//优先级队列比较规则
struct comp
{
bool operator()(const T& lhs,const T& rhs) noexcept
{
return lhs > rhs;
}
};
//迪杰斯特拉算法实现
void dijkstra(int start) noexcept
{
//创建一个空的优先队列Q,将起点加入Q中并设置起点到自身的距离为0,Q中优先级是起点到Q中每一点的距离越短越优先!!!
priority_queue<T,vector<T>,comp> Q;
Q.push(T(start,0));
//创建一个数组dist,用于保存起点到各个节点的距离,初始化为无穷大;
vector<int> dist(n,INT_MAX);
dist[start] = 0;
//创建一个数组visited,用于标记节点是否被访问过,初始化为false;
vector<bool> visited(n,false);
//当Q不为空时,重复以下步骤
while(!Q.empty())
{
//从Q中取出距离起点最近的节点i
T i = Q.top();
Q.pop();
//如果节点i已经被访问过,则跳过此次循环
if(visited[i.v])
{
continue;
}
//i没有被访问则标记为已访问
visited[i.v] = true;
//对于i的每一个邻居节点j,如果i到j有路径且j没有被访问过且i到j的距离小于dist[j],则更新dist[j]的值为dist[j] = min((i到j的距离) + dist[i],dist[j]),然后把节点j加入到Q中
for(size_t j = 0;j < n;++j)
{
if(graph[i.v][j] > 0 && !visited[j] && graph[i.v][j] < dist[j])
{
dist[j] = min(graph[i.v][j] + dist[i.v],dist[j]);
Q.push(T(j,dist[j]));
}
}
}
//输出算法结果
for(size_t i = 0;i < dist.size();++i)
{
cout << start << " -> " << i << " = " << dist[i] << endl;
}
}
int main()
{
init();
for(int i = 0;i < n;++i)
{
dijkstra(i);
cout << endl;
}
return 0;
}

Comments NOTHING