哈夫曼树(Huffman树)实现_一叶飘落尽知秋的博客-CSDN博客_哈夫曼树的实现
定义、
赫夫曼树,别名“哈夫曼树”、“最优树”以及“最优二叉树”。
给定N个权值作为N个叶子结点,构造一棵二叉树,若该树的带权路径长度达到最小,称这样的二叉树为最优二叉树,也称为哈夫曼树(Huffman Tree)。哈夫曼树是带权路径长度最短的树,权值较大的结点离根较近。
一些概念、
路径:在一棵树中,一个结点到另一个结点之间的通路,称为路径。
路径长度:在一条路径中,每经过一个结点,路径长度都要加 1 。例如在一棵树中,规定根结点所在层数为1层,那么从根结点到第 i 层结点的路径长度为 i - 1 。图 1 中从根结点到结点 c 的路径长度为 3。
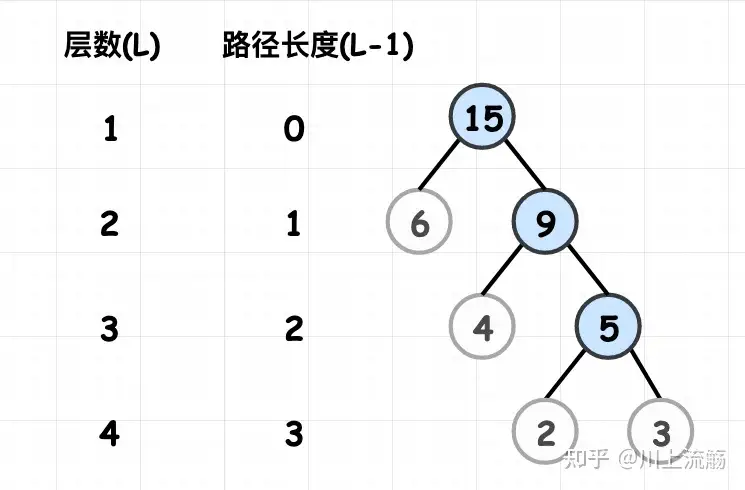
结点的权:给每一个结点赋予一个新的数值,被称为这个结点的权。例如,图 1 中结点 a 的权为 7,结点 b 的权为 5。
结点的带权路径长度:指的是从根结点到该结点之间的路径长度与该结点的权的乘积。例如,图 1 中结点 b 的带权路径长度为 2 * 5 = 10 。
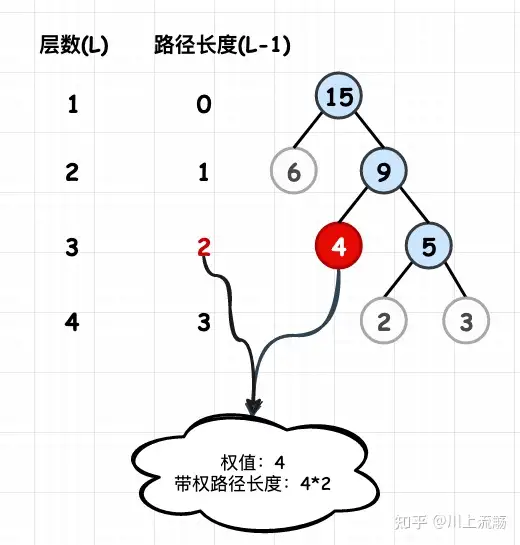
树的带权路径长度为树中所有叶子结点的带权路径长度之和:通常记作 “WPL” 。例如图 1 中所示的这颗树的带权路径长度为:WPL = 7 * 1 + 5 * 2 + 2 * 3 + 4 * 3

构建哈夫曼树、
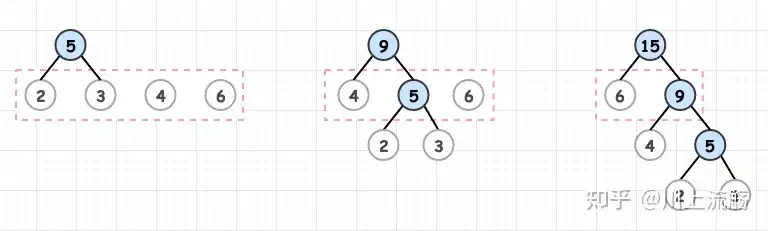
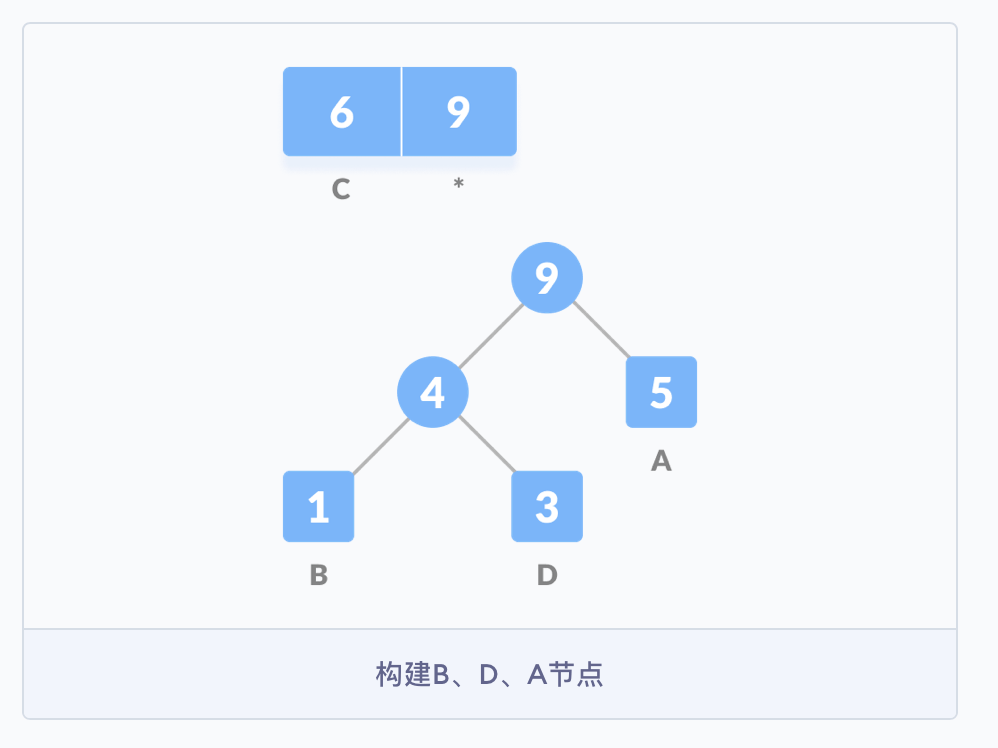
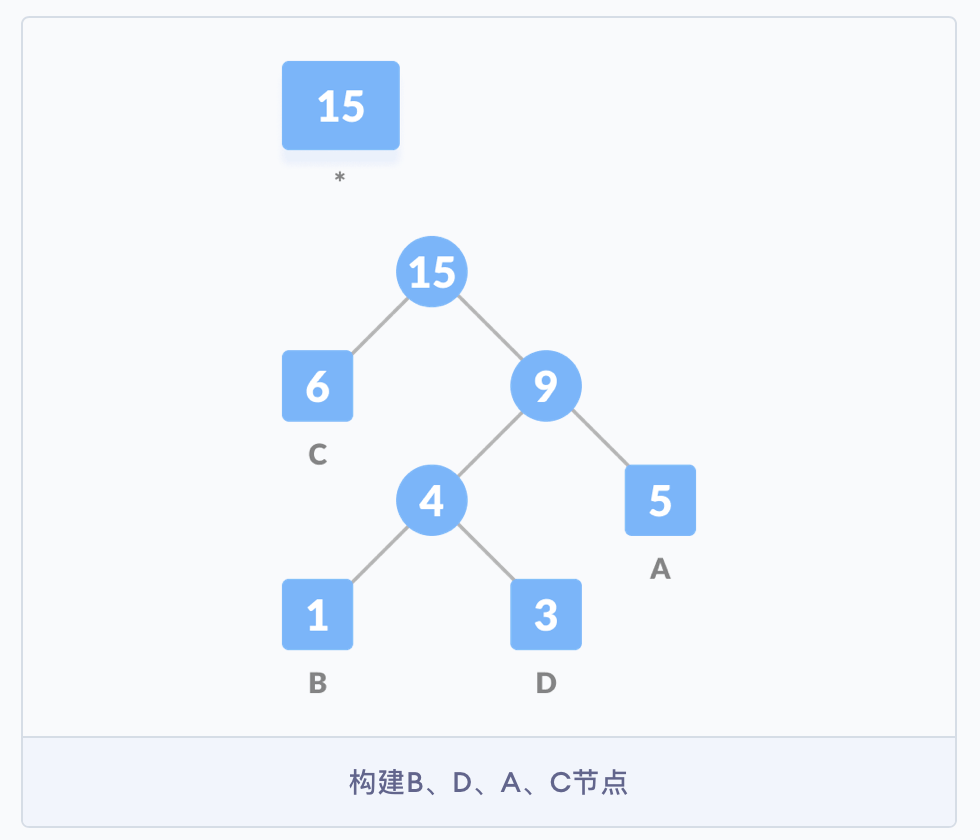
对于给定的有各自权值的 n 个结点,构建哈夫曼树有一个行之有效的办法:
- 在 n 个权值中选出两个最小的权值,对应的两个结点组成一个新的二叉树,且新二叉树的根结点的权值为左右孩子权值的和;
- 在原有的 n 个权值中删除那两个最小的权值,同时将新的权值加入到 n–2 个权值的行列中,以此类推;
- 重复 1 和 2 ,直到所以的结点构建成了一棵二叉树为止,这棵树就是哈夫曼树。
- 例如下面对2,3,4,6四个结点权值构造。
哈夫曼树的应用:哈夫曼编码
哈夫曼编码是一种压缩编码的编码算法,是基于哈夫曼树的一种编码方式。哈夫曼树又称为带权路径长度最短的二叉树。
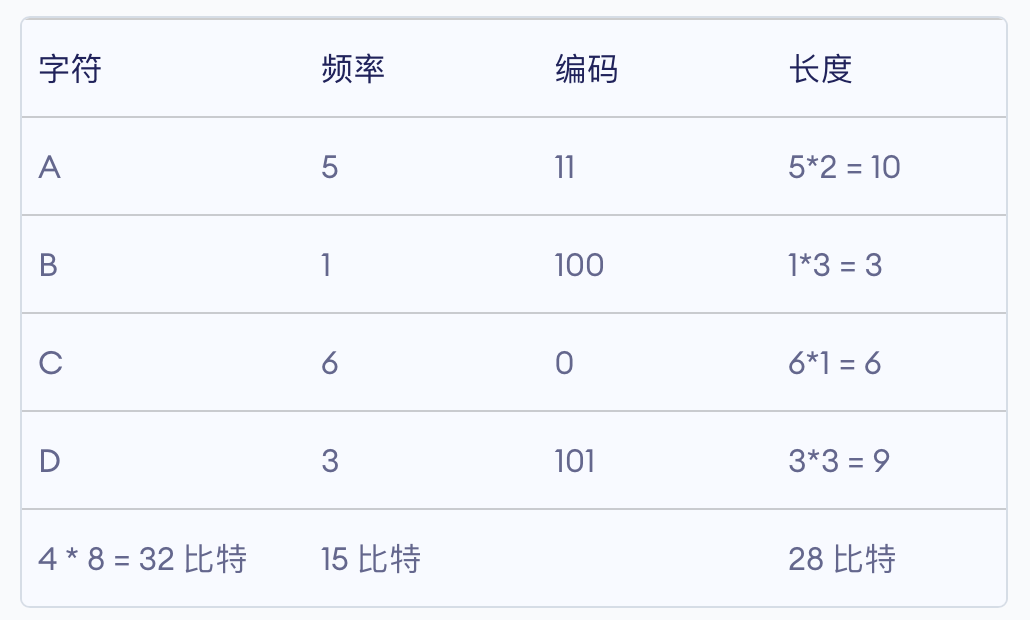
哈夫曼编码首先会使用字符的频率创建一棵树,然后通过这个树的结构为每个字符生成一个特定的编码,出现频率高的字符使用较短的编码,出现频率低的则使用较长的编码,这样就会使编码之后的字符串平均长度降低,从而达到数据无损压缩的目的。
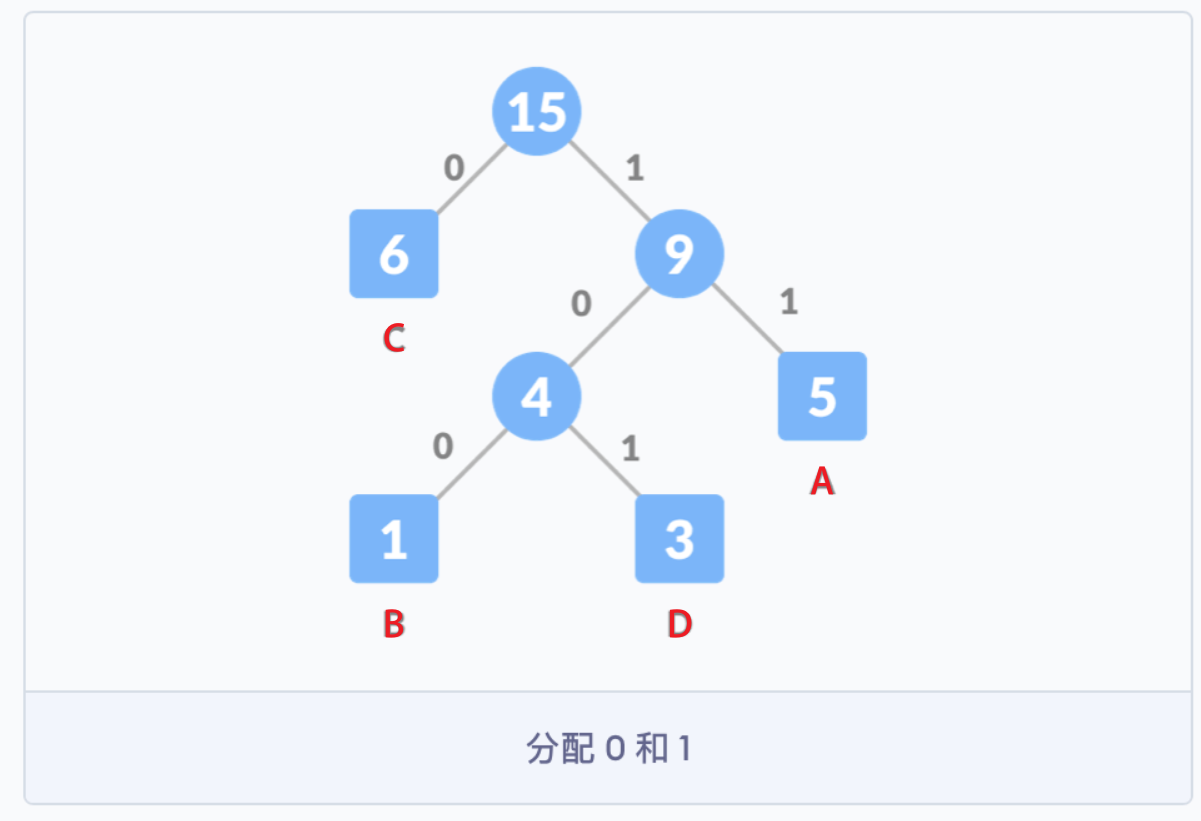
- 1. 计算字符串中每个字符的频率:
- 2. 按照字符出现的频率进行排序,组成一个队列
- 3. 把这些字符作为叶子节点开始构建一颗哈夫曼树
- 4. 对字符进行编码:
为什么通过哈夫曼编码后得到的二进制码不会有前缀的问题呢?
这是因为在哈夫曼树中,每个字母对应的节点都是叶子节点,而他们对应的二进制码是由根节点到各自节点的路径所决定的,正因为是叶子节点,每个节点的路径不可能和其他节点有前缀的关系。
为什么通过哈夫曼编码获得的二进制码短呢?
因为哈夫曼树是带权路径长度最短的树,权值较大的节点离根节点较近。而带权路径长度是指:树中所有的叶子节点的权值乘上其到根节点的路径长度,这与最终的哈夫曼编码总长度成正比关系的。
哈夫曼树和编码都不唯一!只有树的WPL(带权路径长度)才是唯一的!
带权路径长度WPL最短且唯一;编码互不为前缀(一个编码不是另一个编码的开头)。
哈夫曼树实现、
构建哈夫曼树时,首先需要确定树中结点的构成。由于哈夫曼树的构建是从叶子结点开始,不断地构建新的父结点,直至树根,所以结点中应包含指向父结点的指针。但是在使用哈夫曼树时是从树根开始,根据需求遍历树中的结点,因此每个结点需要有指向其左孩子和右孩子的指针,且叶子结点还有权值,和编码的字符,这个权值可以代表编码字符出现的频率。



#include<iostream>
#define _CRTDBG_MAP_ALLOC
using namespace std;
#include<crtdbg.h>
#include<cassert>
#include<type_traits>
#include<vector>
#include<queue>
#include<format>
#include<algorithm>
#include<map>
#include<string>
void optimizeIOstreamAndCheckLeakMemory()
{
_CrtSetDbgFlag(33);
ios::sync_with_stdio(false);
cin.tie(0);
}
class HuffmanTreeNode
{
public:
HuffmanTreeNode(size_t value = 0,char s = '\0') :left(nullptr), right(nullptr), parent(nullptr), value(value), s(s) {}
~HuffmanTreeNode()noexcept{}
HuffmanTreeNode* left; //左孩子
HuffmanTreeNode* right; //右孩子
HuffmanTreeNode* parent; //父结点
size_t value; //结点权值,可以代表编码字符出现的频率
char s; //代表编码的字符
};
class Compare
{
public:
bool operator()(HuffmanTreeNode*p1, HuffmanTreeNode*p2)
{
return p1->value > p2->value; //按照结点权值,编码字符出现的频率从小到大排序
}
};
class HuffmanTree
{
public:
HuffmanTree(const map<char,size_t>&m):_root(nullptr)
{
try {
while (!nodes.empty())
{
nodes.pop();
}
for (const auto&c:m)
{
//传入一个map,表示字符和字符出现的频率
nodes.push(new HuffmanTreeNode(c.second,c.first));
}
}
catch(...){}
}
HuffmanTree(const HuffmanTreeNode& rhs) = delete;
HuffmanTreeNode& operator=(const HuffmanTreeNode& rhs) = delete;
~HuffmanTree()noexcept
{
try
{
destroyTreeNode(_root);
}
catch (...)
{
}
}
void createHuffmanTree()
{
try {
HuffmanTreeNode* p1 = nullptr;
HuffmanTreeNode* p2 = nullptr;
HuffmanTreeNode* cur = nullptr;
while (nodes.size() > 1)
{
p1 = nodes.top(); //第一个最小值结点指针
nodes.pop(); // 出队
p2 = nodes.top(); //第二个最小值结点指针
nodes.pop(); // 出队
cur = new HuffmanTreeNode(p1->value + p2->value); //构造父节点
cur->left = p1; //连接指针
cur->right = p2; //连接指针
p1->parent = cur; //连接指针
p2->parent = cur; //连接指针
nodes.push(cur); //父节点指针入队
}
_root = nodes.top(); //优先队列第一个元素为根节点指针
nodes.pop();
}
catch (...) {}
}
void destroyTreeNode(HuffmanTreeNode* p)
{
if (p == nullptr)
{
return;
}
destroyTreeNode(p->left);
destroyTreeNode(p->right);
delete p;
}
void preOrder (const HuffmanTreeNode* p)const
{
if (p == nullptr)
{
return;
}
cout << p->value << " ";
preOrder(p->left);
preOrder(p->right);
}
void inOrder(const HuffmanTreeNode* p)const
{
if (p == nullptr)
{
return;
}
inOrder(p->left);
cout << p->value << " ";
inOrder(p->right);
}
void postOrder(const HuffmanTreeNode* p)const
{
if (p == nullptr)
{
return;
}
postOrder(p->left);
postOrder(p->right);
cout << p->value << " ";
}
void encode(const HuffmanTreeNode*p,string& code)const
{
if (p->left == nullptr && p->right == nullptr)
{
cout << format("{0} 出现的频率为:{2} 被编码为:{1}", p->s, code,p->value) << endl;
}
if (p->left)
{
code += '0';
encode(p->left, code);
code.erase(code.end() - 1);
}
if (p->right)
{
code += '1';
encode(p->right, code);
code.erase(code.end() - 1);
}
}
const HuffmanTreeNode* root()const
{
return _root;
}
private:
HuffmanTreeNode* _root;
priority_queue<HuffmanTreeNode*, vector<HuffmanTreeNode*>,Compare>nodes;
//按照value值从小到大排列的优先级指针队列,使用优先级队列很巧妙的思想,牛
};
int main()
{
optimizeIOstreamAndCheckLeakMemory();
char str[] = "BCAADDDCCACACAC"; //待测的字符串
map<char, size_t> m; //使用map来保存字符和字符频率的关系
size_t counts = 0; //字符频率
size_t len = strlen(str); //字符串长度
//下面的是测字符的频率,并加到对应的map中
for (char start = 'a'; start <= 'z'; ++start)
{
counts = count(str, str+len, start);
if (counts != 0)
{
m.emplace(pair<char, size_t>(start, counts));
}
}
for (char start = '0'; start <= '9'; ++start)
{
counts = count(str, str + len, start);
if (counts != 0)
{
m.emplace(pair<char, size_t>(start, counts));
}
}
for (char start = 'A'; start <= 'Z'; ++start)
{
counts = count(str, str + len, start);
if (counts != 0)
{
m.emplace(pair<char, size_t>(start, counts));
}
}
HuffmanTree h(m);
h.createHuffmanTree();
cout << format("{0} 的哈夫曼编码如下:", str) << endl;
string s;
h.encode(h.root(), s);
cout << endl;
cout << "哈夫曼树的遍历如下:" << endl;
cout << "先序遍历:" << endl;
h.preOrder(h.root());
cout << endl;
cout << "中序遍历:" << endl;
h.inOrder(h.root());
cout << endl;
cout << "后序遍历:" << endl;
h.postOrder(h.root());
return 0;
}


Comments NOTHING