树状数组

介绍、

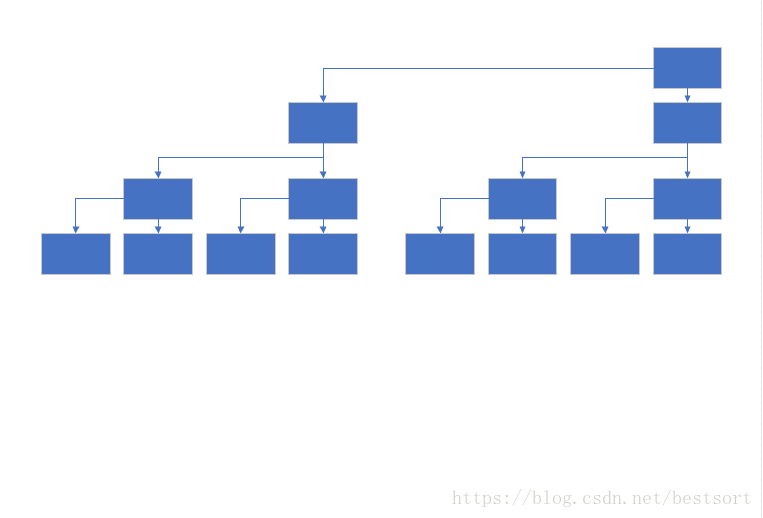
树状数组或二叉索引树（Binary Indexed Tree），又以其发明者命名为 Fenwick 树。其初衷是解决数据压缩里的累积频率的计算问题，现多用于高效计算数列的前缀和、区间和。它可以以 O(logn) 的时间得到任意前缀和。并同时支持在 O(logn) 时间内支持动态单点值的修改。空间复杂度 O(n)。

树状数组是一个查询和修改复杂度都为log(n)的数据结构。主要用于数组的单点修改&&区间求和，另外一个拥有类似功能的是线段树。

具体区别和联系如下：

• 1.两者在复杂度上同级, 但是树状数组的常数明显优于线段树, 其编程复杂度也远小于线段树.
• 2.树状数组的作用被线段树完全涵盖, 凡是可以使用树状数组解决的问题, 使用线段树一定可以解决, 但是线段树能够解决的问题树状数组未必能够解决.
• 3.树状数组的突出特点是其编程的极端简洁性, 使用lowbit技术可以在很短的几步操作中完成树状数组的核心操作，其代码效率远高于线段树。

学习：数据结构----树状数组

树状数组详解

使用、

（1）lowbit（） 运算：它表示非负整数在二进制表示下最低位1和后面的0构成的十进制数值

如 lowbit（44）= lowbit（00101100）= （100） = 4

class NumArray
{
public:
    NumArray(int n):n(n), array(new int[n] {}), tree(new int[n + 1] {})
    {
        //初始化待维护数组
        for (int i = 0; i < n; ++i)
        {
            array[i] = i;
        }

        //树状数组先初始化为0
        memset(tree, 0, sizeof(int) * (n + 1));

        //树状数组初始化
        for (int i = 1; i < n + 1; ++i)
        {
            update(i, array[i - 1], n + 1);
        }
    }

    ~NumArray()noexcept
    {
        delete[] array;
        delete[] tree;
        array = nullptr;
        tree = nullptr;
    }

    //lowbit 操作
    int lowbit(int x)
    {
        return x & -x;
    }

    //求前缀和操作，范围为[1,x]
    int sum(int x)
    {
        assert(x <= n && x > 0);
        int ans = 0;
        for (int i = x; i > 0; i -= lowbit(i)) 
        {
            ans += tree[i];
        }
        return ans;
    }

    //求前缀和操作，范围为[x,y]
    int sum(int x, int y)
    {
        return sum(y) - sum(x - 1);
    }

    //　从单点修改也可以看出为什么树状数组的初始序列的下标要从1开始，如果从0开始的话，
    //lowerbit(0)=0，0+0=0，这样单点修改的程序将一直循环下去。
    //val是值变化量

    void update(int pos, int val,int n)                            
    {
        for (int i = pos; i < n; i += lowbit(i))
        {
            tree[i] += val;
        }
    }

    //打印树状数组
    void print()
    {
        for (int i = 1; i < n + 1; ++i)
        {
            cout << tree[i] << "  ";
        }
        cout << endl;
    }

private:
    int* array;
    int* tree;
    int n;
};