文法介绍:Introduction to Formal Grammars - YouTube
自上而下的解析器使用的上下文无关文法(CFG)要求是没有歧义、不含左递归,并且是确定性的。没有歧义的CFG意味着对于给定的输入,解析器可以唯一地确定一棵语法树。不含左递归的CFG是为了避免解析器陷入无限循环。确定性的CFG意味着对于任何给定的非终结符和输入符号,只能有一个产生式可以被应用。这些要求有助于确保解析器能够正确地解析输入并生成正确的语法树。

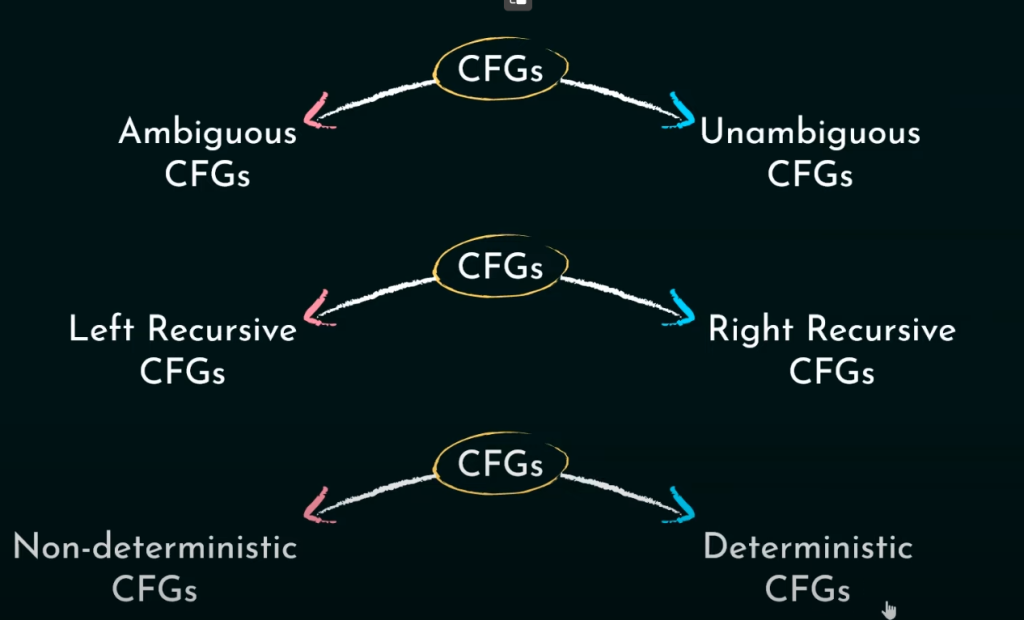
文法有四种类型,主要关注上下文无关语法!!!

上下文无关语法通式是 A-> α; 规定左侧只有一个非终结符,右侧的α是 P 和 N 的任意元素组成的集合;

语法分析使用CFG和token流生成语法树。

CFG类型、
推导方式、

根据CFG推导id + id × id 有三种方法,左推导和右推导和解析树推导。
左推导就是从左往右推导;右推导就是从右往左推导;还有建立解析树推导,遍历时从上到下,从左到右取终结符得到推导式!!!
歧义、

还是上图,同样的规则同样的结果,推导方式却有多个,这就叫做歧义。
对于任意CFG语法,如果我们有多个左推导或者右推导或者解析树,那么这是不明确的;如果是明确的,则应该只有一个唯一的推导方式。
有歧义的CFG文法可能会导致编译器无法接受。编译器通常需要文法是无歧义的,以便能够准确地解析语法。如果文法存在歧义,编译器可能无法确定正确的解析方式,从而导致编译错误或者产生错误的结果。因此,在设计文法时,需要尽量避免歧义,以确保编译器能够正确地解析语法。
优先级问题、
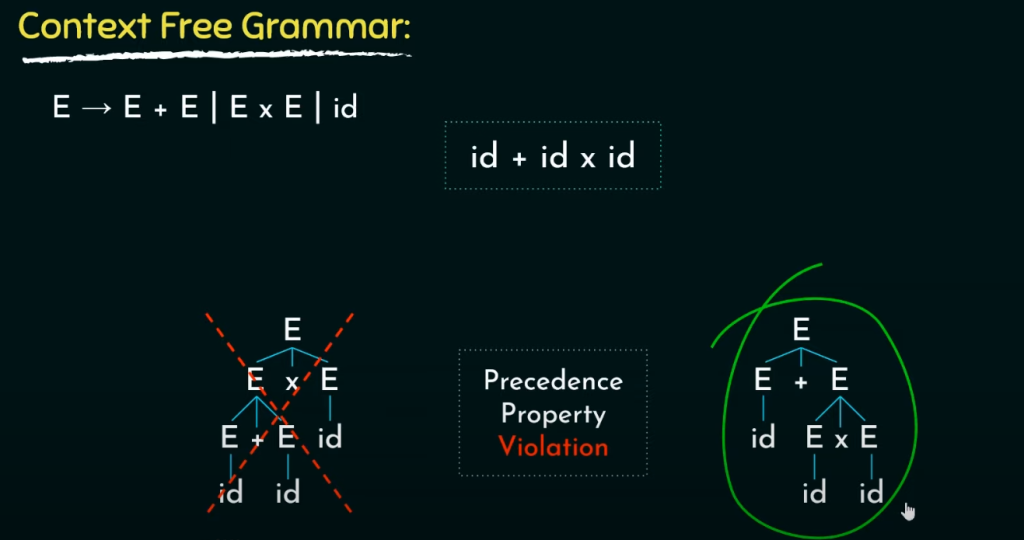
歧义问题能够引出优先级问题,根据优先级,乘法优先级大于加法,乘法所在层次应该大于加法所在层次!!!我们要修改规则,推导出正确的解析树。
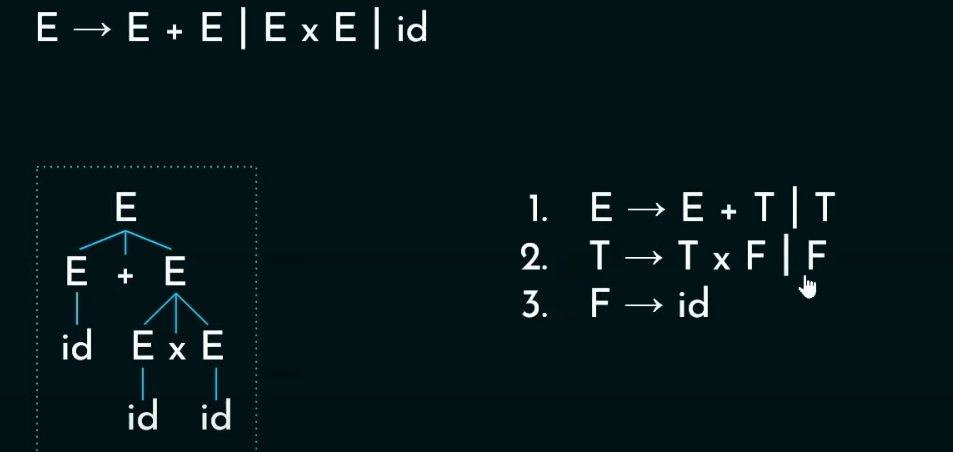
由于加法和乘法都是左结合,因此我们要替换右边的非终结符,这样就能保住在加法前推导出乘法。
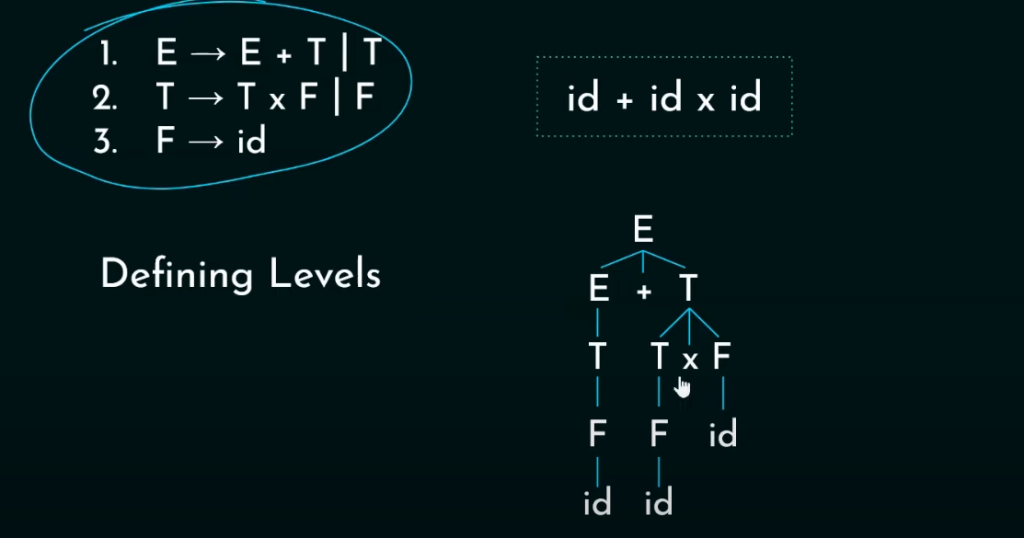
优先级和结合性问题、


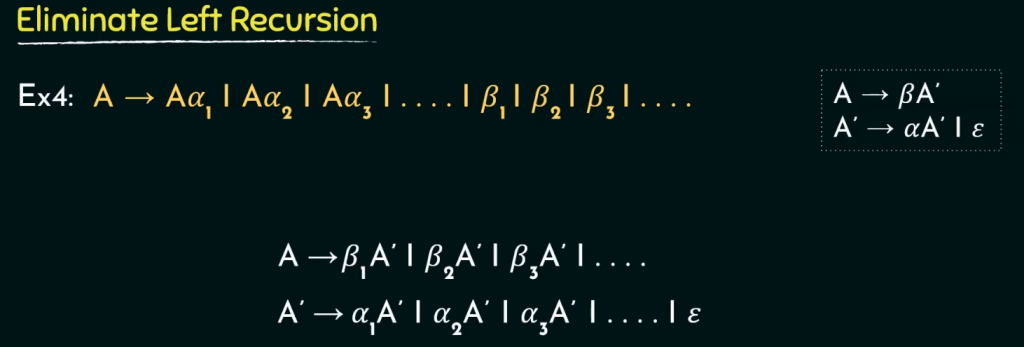
递归、
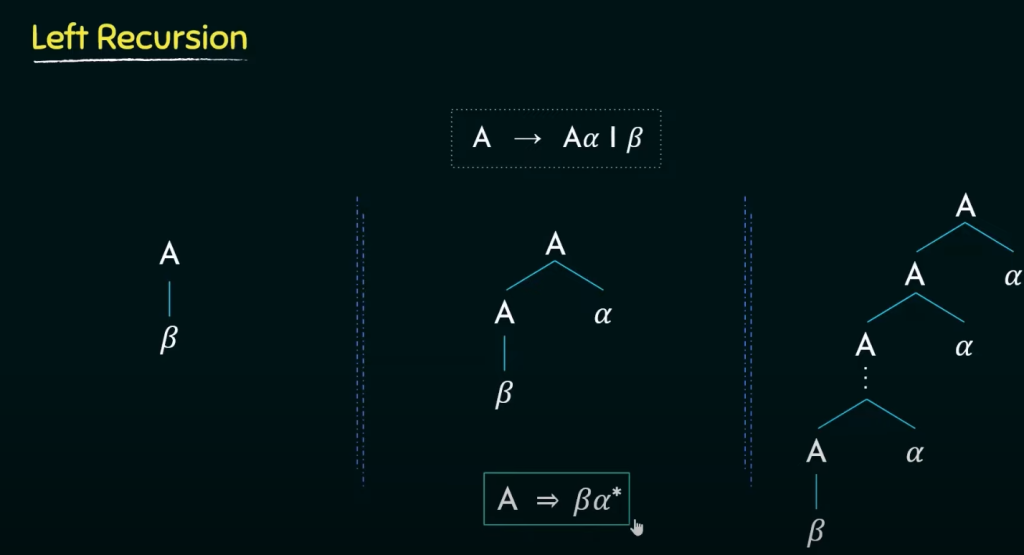


左递归会一直调用自身,导致混乱,所以要把左递归转换为右递归!!!
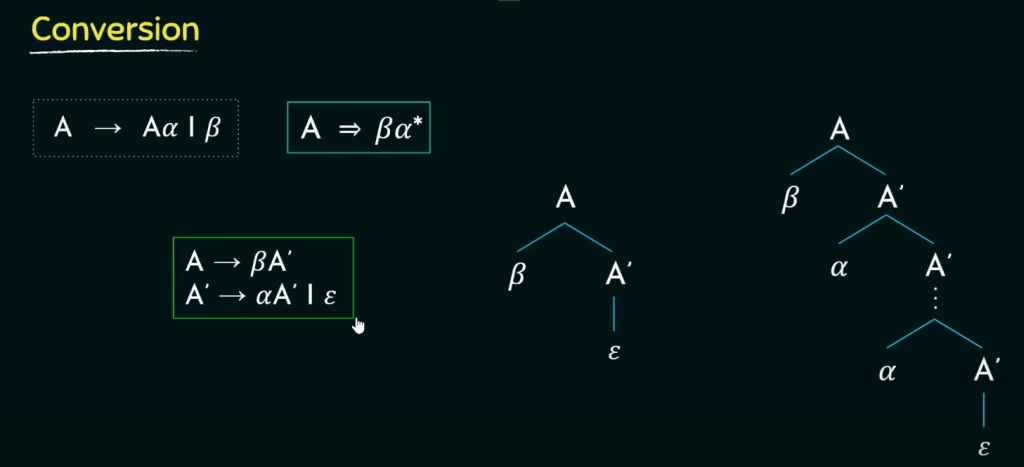
上述就是转换规则!!!
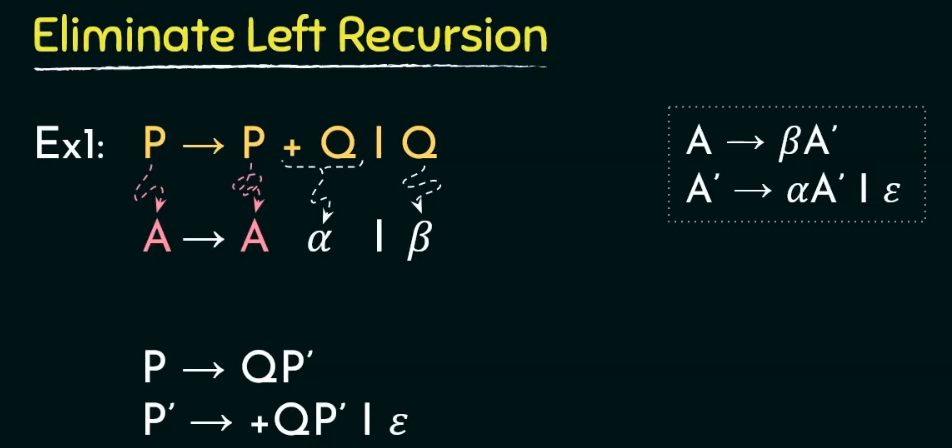

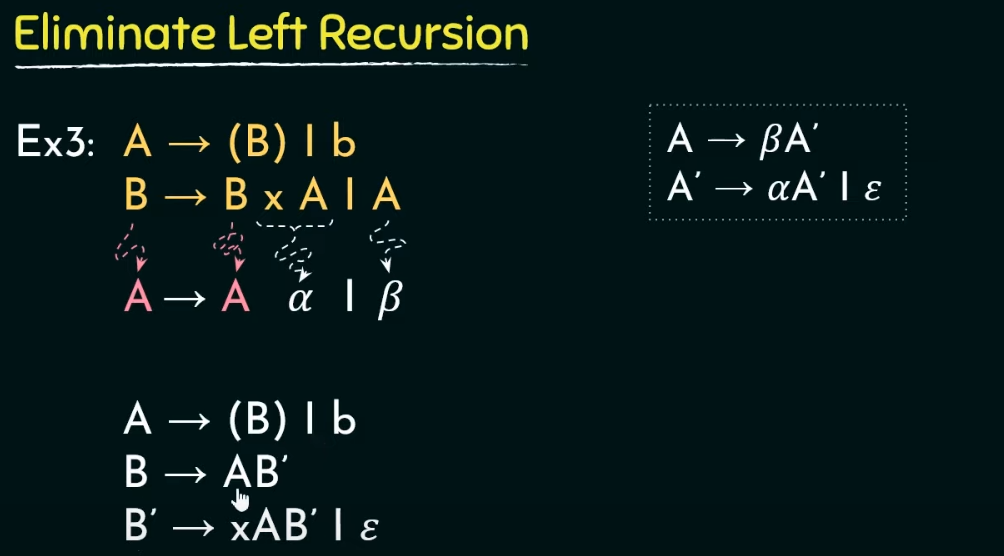
不确定性、
Non-Deterministic CFGs - YouTube




确定性和歧义、
- 确定性(Determinism): 一个CFG被称为是确定性的,如果对于每个非终结符的每个产生式,至多只有一个产生式能够匹配给定的输入。换句话说,在给定一个非终结符和一个输入串的情况下,不会存在多个可选的产生式。确定性的CFG对于语法分析和编译器的实现非常重要,因为它们能够确保在解析时只有一种正确的推导路径。
- 歧义(Ambiguity): 歧义指的是一个CFG能够生成同一个句子的多个不同的推导路径。换句话说,同一个句子可以被解释成多种语法结构。这在语言理解和翻译中是一个问题,因为它会导致多义性,使得解析和理解句子的含义变得困难。一些自然语言中的句子经常会涉及歧义,这使得语法分析变得复杂。
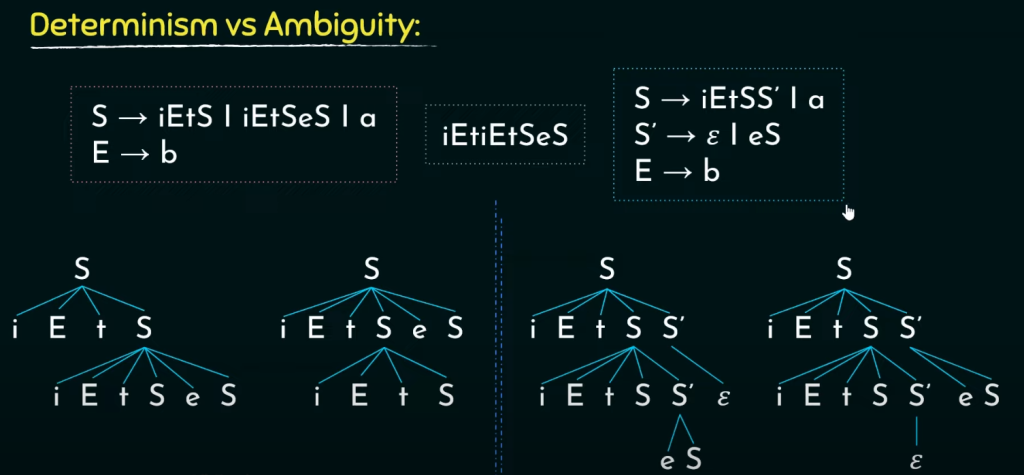
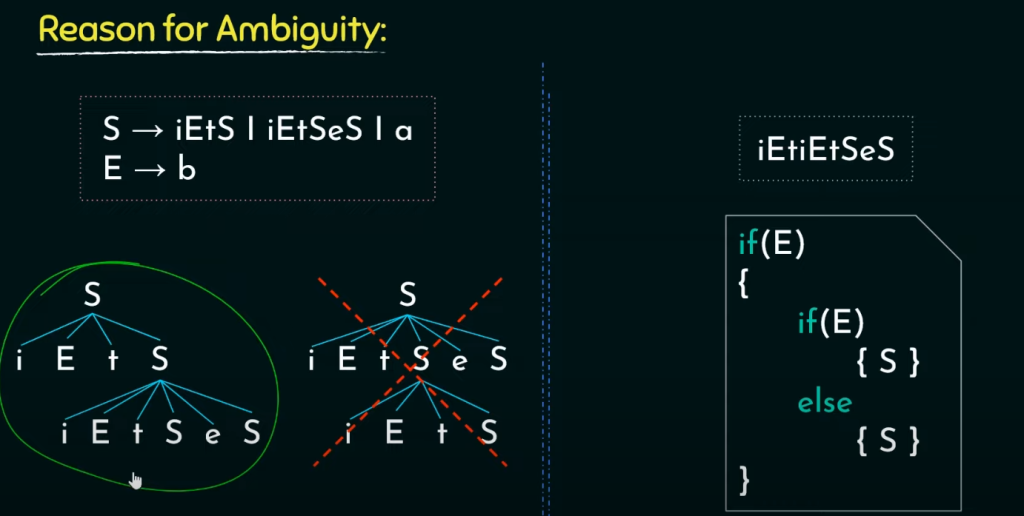
即使是确定的CFG也不能保证推导出的语句过程没有歧义!!!


Comments NOTHING