概念:
也许因为输入值不够随机,也许因为经过某些插入或删除操作,二叉搜索树可能会失去平衡,造成搜索效率低的情况,如下图所示:
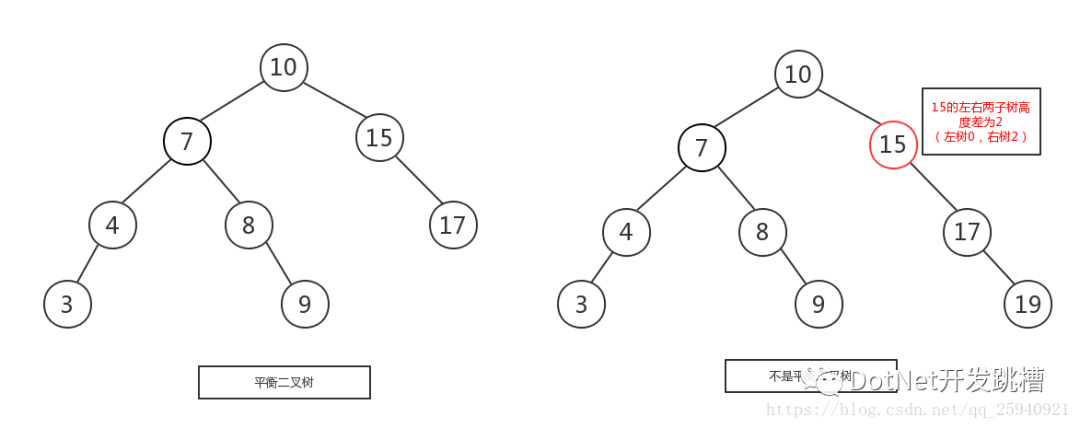
所谓树形平衡与否,并没有一个绝对的测量标准。平衡的大致意义是:没有任何一个节点过深即深度过大。不同的平衡条件,造就出不同的效率表现,以及不同的实现复杂度。有数种特殊结构如AVL-tree,RB-tree,AA-tree,均可实现出平衡二叉树,它们都比一般的二叉搜索树复杂,因此,插入节点和删除节点的平均时间也比较长,但是它们可以避免极难应付的最坏情况,而且由于它们总是保持某种程度的平衡,所以元素的访问时间平均而言也就比较少了,一般而言可以节省百分之25左右。
AVL-tree:
AVL-tree是一个“加上了额外平衡条件”的二叉搜索树。其平衡建立是为了确保整颗树的深度为O(logN)。直观上的最佳平衡条件是每个节点的左右子树有着相同的高度,但这未免太过严苛,我们很难插入新元素而又保持这样的平衡条件。AVL-tree于是退而求其次,要求任何节点的左右子树高度相差最多一。这是一个较弱的条件,但也能保证“对数深度”平衡状态。
下图是一个AVL-tree,但是插入节点11后就不是平衡树了,因为22节点的左节点深度为4,右节点深度为2,超过了1了。
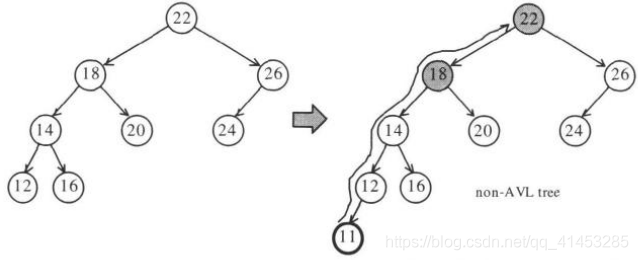
调整AVL-tree:
如果是添加、删除节点导致一个AVL tree变为非AVL tree。只要调整“插入点至根节点”路径上、平衡状态被破坏之各节点中最深的那一个,便可使整棵树重新获得平衡
假设该最深节点为X,由于节点最多拥有两个子节点,而所谓“平衡被破坏”意味着X的左右两棵子树的高度相差2,因此我们可以轻易将情况分为4种:
1.插入点位于X的左子节点的左子树——左左
2.插入点位于X的左子节点的右子树——左右
3.插入点位于X的右子节点的左子树——右左
4.插入点位于X的右子节点的右子树——右右
情况1,4彼此对称,称为外侧(outside)插入,可以采用单旋转操作调整解决
情况2,3彼此对称,称为内侧(inside)插入,可以采用双旋转操作调整解决
具体的旋转方向根据不平衡节点的左右子树的深度进行考虑,由深度较大的一方向深度较小的一方旋转。

旋转:
旋转超详细解析网址:红黑树变色和旋转,图文案例超详细解析
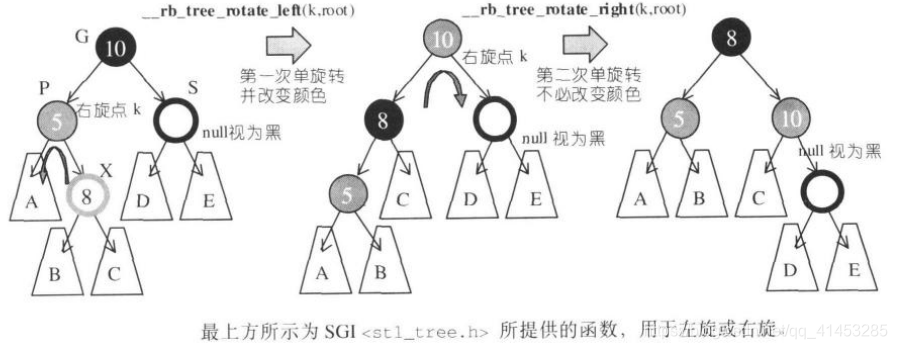
接下来我们再来看如何通过旋转来调整红黑树,在说之前,有必要先来了解下旋转的基础操作左旋和右旋,看图:
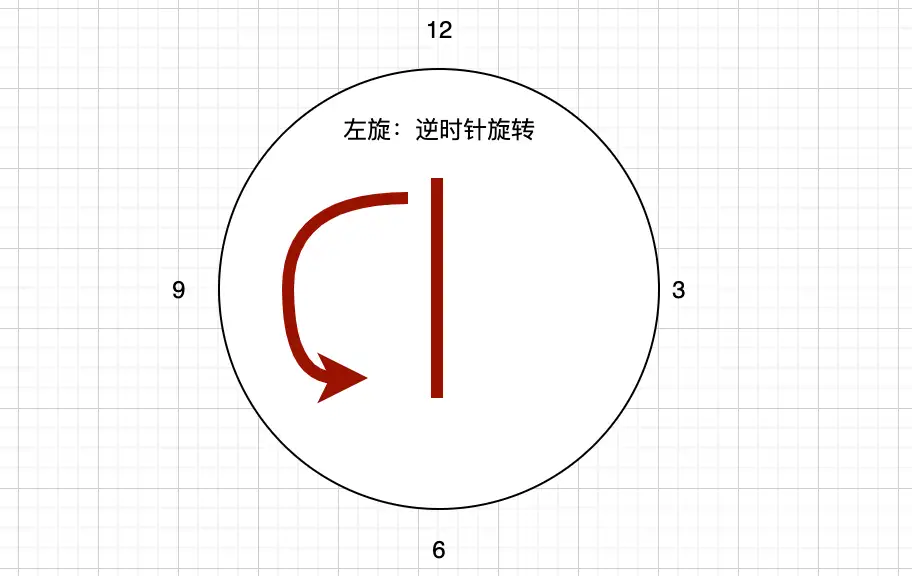
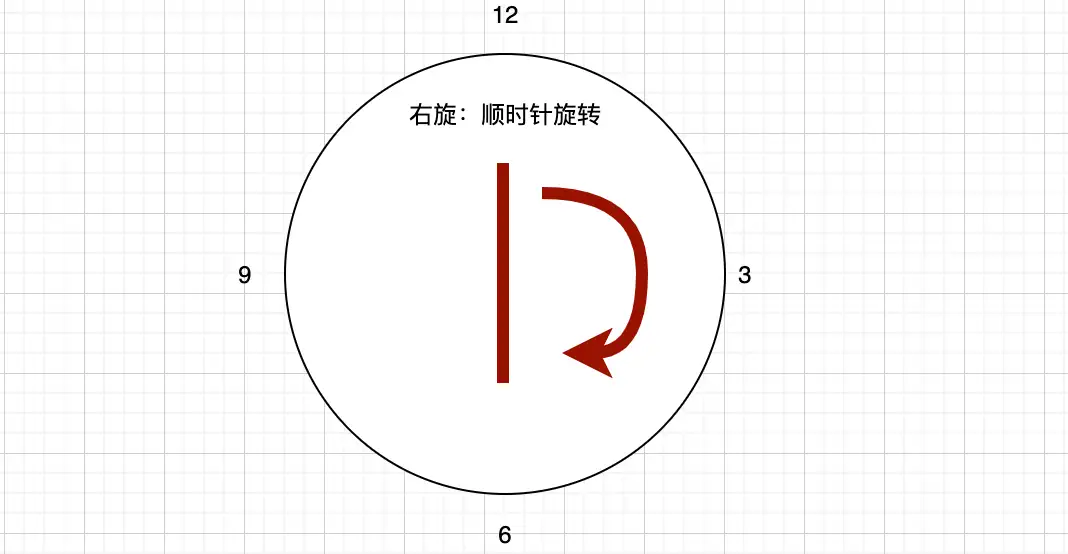
这里有个左右旋的口诀:
左旋:左右左,也就是左旋是把该节点作为其右孩子的左孩子
右旋:右左右,也就是右旋就是把该节点作为其左孩子的右孩子
看个例子:
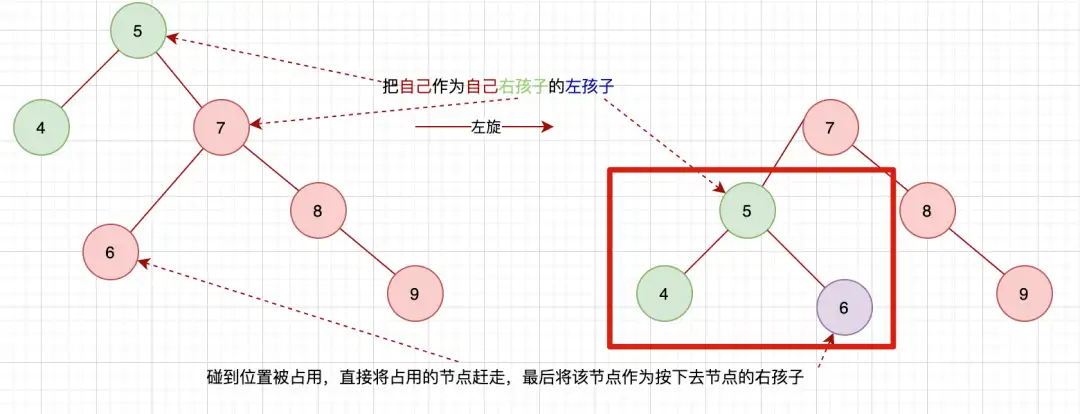
以上就是一个左旋的案例,也就是对节点5进行左旋,根据口诀“左右左”,就是对节点5左旋,然后将节点5作为自己右孩子节点7的左孩子,这里会遇到位置被占用的情况,那这个时候的做法就是将占用位置的节点6作为节点5的右孩子!
所以把口诀补充一下就是:
左旋:左 - 右 - 左 - 右(把赶走的节点作为该节点的右孩子)
右旋:右 - 左 - 右 - 左(把赶走的节点作为该节点的左孩子)
关于左右旋,主要的就是先搞懂旋转的方向,然后对旋转的节点依据口诀来操作,这块自己可以多练习一下,就会慢慢体会到口诀的妙处了!
单旋转:
为了调整平衡状态,我们希望将A子树提高一层,并将C子树下降一层,解析如下:
把K1向上提起,使K2自然下滑,并将B子树挂到K2的左侧
因为K2>k1,所以K2必须称为新树中K1的右子节点
未旋转前B位于K1-K2之间,所以旋转之后,B必须位于K1右侧,K2的左侧。也就是对k2进行了右旋转。
下图显示的是“左左”外侧插入,至于“右右”外侧插入也是如此
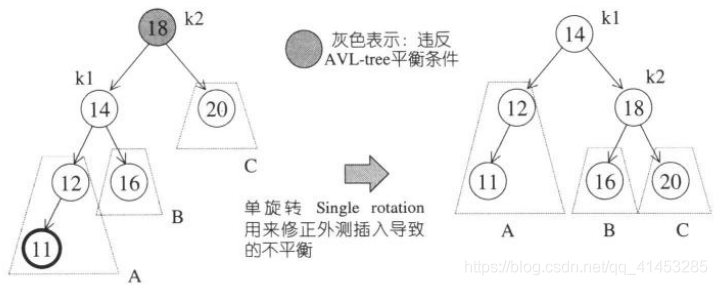
双旋转:
- 下图左侧为内侧插入所造成的不平衡状态
- 单旋转不能解决这种情况:
- 因为,我们不能再以K3为根节点
- 其次,我们不能将K3和K1做一次单旋转,因为旋转之后还是不平衡
- 双旋转可以解决这种情况:
- 以K2为新的根节点
- 这使得K1必须成为K2的左子节点,K3必须成为K2的右子节点

为什么称为双旋转哪,因为它利用两次单旋转,如下图所示
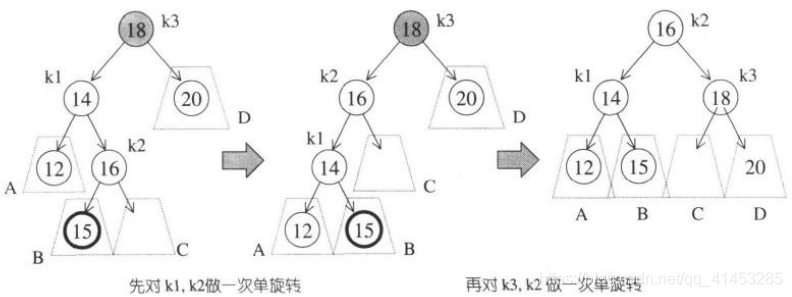
先对k1进行左旋转,然后对k3进行右旋转。
上图显示的是“左右”外侧插入,至于“右左”外侧插入也是如此
RB-tree:
RB-tree是另一个被广泛使用的平衡二叉树,也是SGI STL唯一实现的一种搜索树,作为关联式容器的底层机制作用。RB-tree的平衡条件虽然不同于AVL-tree,但同样运用了单旋转和双旋转修正操作。
RB-tree必须满足以下规则:
1)每个节点不是红色就是黑色
2)根节点为黑色
3)如果节点为红,其子节点必为黑
4)任一节点至NULL(树尾端)的任何路径,所含之黑节点数必须相同
5)默认将空节点作为叶子结点,且是黑色

RB-tree的插入节点:
现在让我们延续上图的状态,插入一些新节点,看看会发生什么变化。我们列举出四种不同的类型。
为了方便讨论,让我先为某些特殊节点定义一些别名。以下讨论都将沿用这些代名。假设新节点为X,其父节点为P,祖父节点为G,伯父节点(父节点的兄弟节点)为S,曾祖父节点为GG。现在根据二叉搜索树的规则,新节点X必是叶节点。根据红黑树规则4,X必为宏。若P也为红(则就违反了规则3,必须调整树形),则G必为黑。于是根据X的插入位置及外围节点的颜色,有了斜面四种考虑。默认插入的新节点为红色,因为黑色会改变平衡。
状况1:
S为黑且X为外侧插入。对此情况,我们先对G做一次右旋转,并更改P,G颜色,即可重新满足红黑树的规则3,
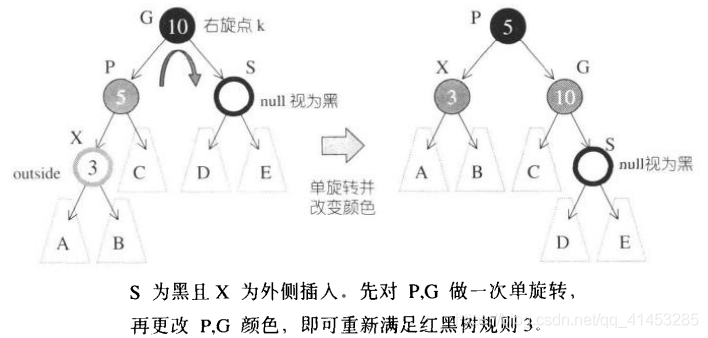
注意,此时可能产生不平衡状态,即某节点左右子树高度相差一以上。这倒没关系,因为RB-tree的平衡性本来就比AVL-tree弱。然和RB-tree通常能够导致良好的平衡状态。是的,经验告诉我们,RB-tree的搜索平均效率和AVL-tree几乎相等。
状况2:
S为黑且X为内侧插入。对此情况,我们必须先对P做一次左旋转,并更改G,X颜色,在将结果对G做一次右旋转,即可再次满足红黑树规则三。
状况3:
S为红且X为外侧插入。对此情况,先对G做一次右旋转,并改变X的颜色。此时如果GG为黑,一切搞定,但如果GG为红,则问题就比较麻烦些,见状况4.

状况4:
S为红且X为外侧插入。对此情况,先对G做一次右旋转,并改变X的颜色,此时如果GG为红,还得持续往上做,直到不再有父子连续为红的情况。
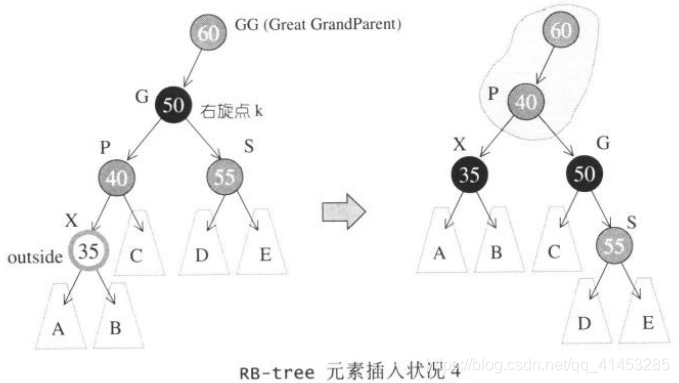
为了避免上面状况④“父子节点都为红色”的情况持续向RB-tree的上层结构发展,形成处理时效率上的瓶颈,我们可以施行一个由上而下的程序:假设新增节点为A,那么就沿着A的路径,只要看到有某节点X的两个子节点都为红色,就把X改为红色,并把两个子节点改为黑色。如下图所示
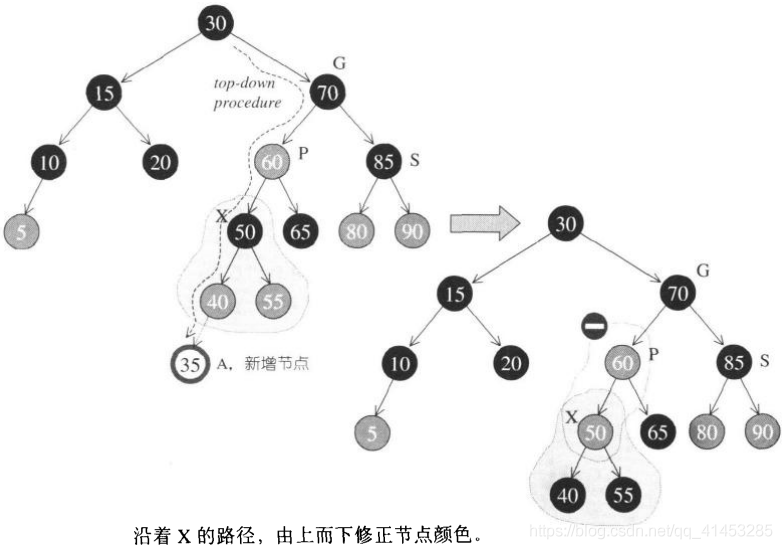
- 但是如果A的父节点P还为红色(注意,此时S绝不可能为红色),就得向状况①一样地做一次单旋转并改变颜色,或是像胡子那个框②一样地做一次双旋转并改变颜色
- 在此之后,节点35的插入就变得简单了:要么直接插入,要么插入后再一次单旋转即可。如下图所示
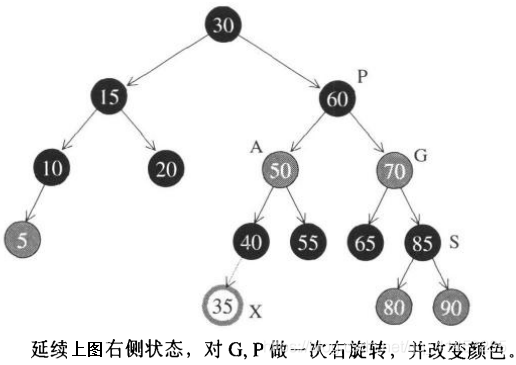
RB-tree的节点设计:
RB-tree有红黑二色,并且拥有左右节点,我们很容易就可以勾勒出其结构风貌。下面是SGI STL的实现源代码。为了有更大的弹性,节点分为两层。
从以下的minimum()和maximum()函数可以看出,RB-tree作为一个二叉搜索树,其极值是多么容易找到。由于RB-tree的各种操作时常需要上溯其父节点,所以特别在数据结构中安排了一个parent指针。
RB-tree的迭代器:
要成功的将RB-tree实现为一个泛型容器,迭代器的设计是一个关键。首先我们要考虑它的类别,然后要考虑它的前进,后退,提领,成员访问等操作。
为了更大的弹性,SGI将RB-tree的迭代器实现分为两层。
RB-tree迭代器属于双向迭代器,但不具备随机定位能力,其提领操作和成员访问操作与list十分类似
注意:
RB-tree迭代器的前进操作operator++()调用的是基类中的increment()函数
RB-tree迭代器的后退操作operator--()调用的是基类中的decrement()函数
前进或后退的行为依据二叉搜索树的节点排列规则,再加上实现上的某些特殊技巧
实现:
RB-tree的部分代码实现,这玩意太难了,现在暂时理解不了,先挖个坑,以后理解了在回来继续写.......
#pragma once
#ifndef _RB_TREE_H_
#define _RB_TREE_H_
using namespace std;
using _rb_tree_color_type = bool; //使用bool值代替红黑色
const _rb_tree_color_type _rb_tree_red = false; //红色为0
const _rb_tree_color_type _rb_tree_black = true; //黑色为1
//RB树节点基类
class _rb_tree_node_base
{
public:
virtual ~_rb_tree_node_base()noexcept{} //虚析构函数
_rb_tree_node_base():color(0),parent(0),left(0),right(0) {}
using color_type = _rb_tree_color_type; //为颜色起别名
using base_ptr = _rb_tree_node_base*; //为节点基类指针起别名
//四个基类成员
color_type color; //节点颜色
base_ptr parent; //提供RB树的许多操作的父节点指针
base_ptr left; //指向左节点
base_ptr right; //指向右节点
//返回最小值的函数
static base_ptr minimum(base_ptr x)
{
while (x->left != 0)
{
x = x->left;
}
return x;
}
//返回最大值的函数
static base_ptr maximum(base_ptr x)
{
while (x->right != 0)
{
x = x->right;
}
return x;
}
};
//RB树节点的实现,继承基类
template<class Value>
class _rb_tree_node :public _rb_tree_node_base
{
public:
_rb_tree_node():_rb_tree_node_base(){}
~_rb_tree_node()noexcept{}
using link_type = _rb_tree_node<Value>*; //link_type是一个树节点指针
//树节点的一个成员加上基类继承的四个共计五个成员
//树节点基类保存有调整树的指针,而节点类实际上只保存节点值
//调整时可以通过基类来调整
Value value_filed; //节点值
private:
};
//树迭代器基类
class _rb_tree_iterator_base
{
public:
using base_ptr = _rb_tree_node_base::base_ptr; //使用树节点基类的指针
using iterator_category = bidirectional_iterator_tag; //不知道什么东西,标准库自带的
using difference_type = ptrdiff_t; //为指针距离起别名
virtual ~_rb_tree_iterator_base()noexcept{}
_rb_tree_iterator_base():node(0){} //默认构造函数,初始化为0
//实际的迭代器基类成员
base_ptr node; //一个node基类的指针,用来与容器之间产生一个连结关系
//以下其实可实现于operator++内,因为再无他处会调用此函数了
void increment()
{
if (node->right != 0) //如果有右节点,状况1
{
node = node->right; //往右走
while (node->left != 0) //然后一直往左子树走到底
{
node = node->left; //即是解答
}
}
else
{
base_ptr y = node->parent;
while (node == y->right)
{
node = y;
y = y->parent;
}
if (node->right != y)
{
node = y;
}
}
}
//以下其实可实现于operator--内,因为再无他处会调用此函数了
void decrement()
{
if (node->color == _rb_tree_red && node->parent->parent == node)
{
node = node->right;
}
else if (node->left != 0)
{
base_ptr y = node->left;
while (y->right != 0)
{
y = y->right;
}
node = y;
}
else
{
base_ptr y = node->parent;
while (node == y->left)
{
node = y;
y = y->parent;
}
node = y;
}
}
};
//迭代器的实现.继承基类
template<class Value,class Ref,class Ptr>
class _rb_tree_iterator:public _rb_tree_iterator_base
{
public:
//迭代器的实际成员是一个树节点基类指针node
using link_type = _rb_tree_node<Value>*; //这个link_type是树节点的指针
using value_type = Value; //value值
using reference = Ref; //不清楚为什么要这样写
using pointer = Ptr; //不清楚为什么要这样写
using iterator = _rb_tree_iterator<Value, Value&, Value*>; //不清楚为什么要这样写
using const_iterator = _rb_tree_iterator<Value, const Value&, const Value*>; //不清楚为什么要这样写
using self = _rb_tree_iterator<Value, Ref, Ptr>; //不清楚为什么要这样写
_rb_tree_iterator():_rb_tree_iterator_base(){} //默认构造函数,初始化为0
_rb_tree_iterator(link_type x) :node(x) {} //有参构造函数,使用一个树节点的指针来初始化自身的树基类指针
_rb_tree_iterator(const iterator&it):node(it.node) {} //拷贝构造函数
~_rb_tree_iterator()noexcept {}
reference operator*()const
{
return link_type(node)->value_filed; //使用一个基类的指针来初始化一个派生类对象
}
pointer operator->()const
{
return &(operator*());
}
self& operator++()
{
increment();
return *this;
}
self operator++(int)
{
self tmp = *this;
decrement();
return tmp;
}
self& operator--()
{
decrement();
return *this;
}
self operator--(int)
{
self tmp = *this;
decrement();
return tmp;
}
};
//RB-tree的实现
template<class Key,class Value,class KetOfValue,class Compare>
class rb_tree
{
protected:
using void_pointer = void*;
using base_ptr = _rb_tree_node_base*;
using rb_tree_node = _rb_tree_node<Value>;
using color_type = _rb_tree_color_type;
public:
using key_type = Key;
using value_type = Value;
using pointer = value_type*;
using const_pointer = const value_type*;
using reference = Value&;
using const_reference = const Value&;
using link_type = _rb_tree_node<Value>*;
using size_type = size_t;
using difference_type = ptrdiff_t;
protected:
static link_type allocate()
{
return static_cast<link_type>(operator new(sizeof(_rb_tree_node<Value>)));
}
void put_node(link_type p)
{
operator delete(p);
}
link_type get_node()
{
return allocate();
}
link_type create_node(const value_type& x)
{
link_type tmp = get_node();
construct_at(&tmp->value_filed, x);
return tmp;
}
link_type clone_node(link_type x)
{
link_type tmp = create_node(x->value_filed);
tmp->color = x->color;
tmp->left = 0;
tmp->right = 0;
return tmp;
}
void destroy_node(link_type p)
{
destroy_at(&p->value_filed);
put_node(p);
}
protected:
//RB-tree 只以三笔数据表现
size_type count; //节点数量
link_type header; //这是实现上的一个小技巧
Compare key_compare; //节点间的键值大小比较准则,是一个函数对象
//以下三个函数用来方便取得header的成员
link_type& root()const
{
return (link_type&)header->parent;
}
};
#endif // ! _RB_TREE_H_


Comments NOTHING