概念:
所谓二叉搜索树(binary search tree),可提供对数时间的元素插入和访问。二叉搜索树的节点放置规则是:任何点的键值一定大于其左子树中的每一个节点的键值,并小于其右子树的每一个节点的键值。因此,从根节点一直往左走,直到无路可走即可获得最小的元素;从根节点一直往右走,直至无路可走,即可获得最大元素。
要在一颗二叉搜索树中找出最大元素和最小元素,是一件极简单的事情:就像上述所言,一直往左走或一直往右走即可。比较麻烦的是元素的插入和删除。插入新元素时,就从根节点开始,遇键值较大者就向左,遇键值较小者就向右,一直到尾端,即为插入点。
下面就是一个二叉搜索树.......
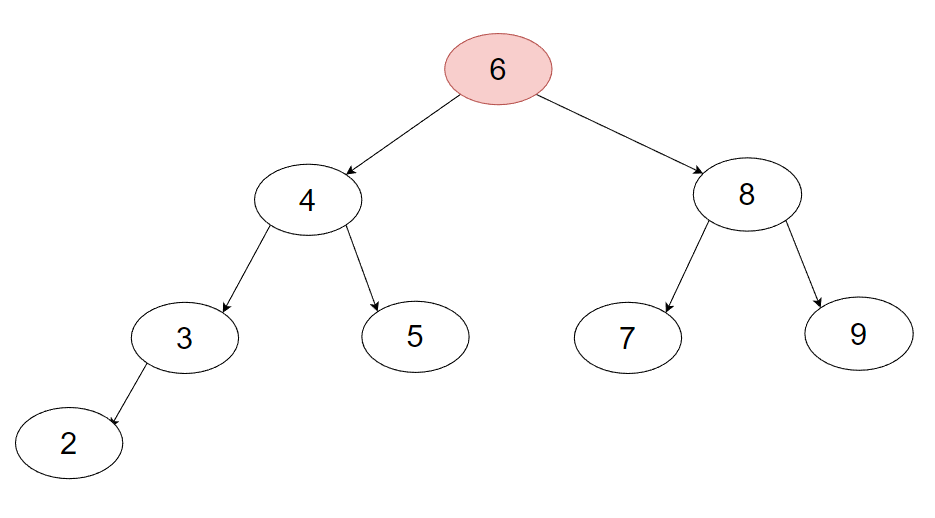
二叉搜索树的删除:
如果想要删除一个节点A,情况可分为两或者三种:
1)如果A只有一个子节点,我们就直接将A的子节点连接至A的父节点,并将A删除。
2)如果A有两个子节点,我们就以右子树内的最小节点取代A。注意右子树的最小节点很容易获得,从右子节点开始,一直往左走即可。
二叉搜索树的查找:
二叉搜索树的查找思路很简单:要找的值比当前节点小就去左子树找,比当前节点大就往右子树找,找到空节点就说明没找到返回false即可。
二叉搜索树的插入:
二叉搜索树的插入和查找差别不大,首先寻找插入位置,比当前节点小就往左子树找,比当前节点大就往右子树找,直到找到空指针时,就可以进行一个插入。
那么要插入的值和当前节点相同该怎么办呢?可以选择将重复的值放在右子树或左子树都可。
二叉搜索树的简单实现:
//编译环境VS2022,C++标准20
//树节点结构体
template<class _Ty>
class _search_tree_node
{
public:
using node = _search_tree_node<_Ty>;
_search_tree_node(){}
~_search_tree_node()noexcept{}
node* left; //有三个成员
node* right;
_Ty data;
};
template<class _Ty>
class search_tree
{
public:
using node = _search_tree_node<_Ty>;
//禁止拷贝赋值
search_tree<_Ty>& operator=(const search_tree<_Ty>& rhs) = delete;
//拷贝构造函数
search_tree(const search_tree<_Ty>& rhs) :_root(0), sizes(0)
{
_root = copy_tree(rhs._root);
sizes = rhs.sizes;
}
//移动构造函数
search_tree(search_tree<_Ty>&& rhs) noexcept :_root(rhs._root), sizes(rhs.sizes)
{
rhs._root = 0;
rhs.sizes = 0;
}
//默认构造函数
search_tree():_root(0),sizes(0){}
//析构函数
~search_tree()noexcept
{
clear();
}
//添加元素方法
void push(const _Ty& value)
{
if (_root == 0) //首先判断是否有根节点
{
_root = allocate_node(); //没有根节点就造一个根节点
construct_node(_root, value);
sizes++;
return;
}
node* cur = _root; //记录_root位置
node* parent = 0; //记录当前节点的父亲节点位置
while (cur) //根据值的大小找出插入的节点位置
{
if (cur->data > value) //节点的值大于value
{
parent = cur; //记录父亲节点位置
cur = cur->left; //往左寻找
}
else if (cur->data <= value) //节点的值小于value
{
parent = cur; //记录父亲节点位置
cur = cur->right; //往右寻找
}
}
cur = allocate_node(); //造出新的节点
construct_node(cur, value); //赋值value
if (parent->data < value) //对父亲节点值进行判断
{
parent->right = cur; //父亲节点值小于value,新节点就在父亲节点的right
sizes++;
}
else
{
parent->left = cur; //父亲节点值大于value,新节点就在父亲节点的left
sizes++;
}
}
//删除指定元素法
void pop(const _Ty&value)
{
//有三种情况
//1.被删除节点有一个孩子
//2.被删除节点有两个孩子
//3.被删除节点没有孩子
node* cur = _root;
node* pre = 0;
//寻找删除位置
while (cur)
{
if (cur->data < value)
{
pre = cur;
cur = cur->right;
}
else if (cur->data > value)
{
pre = cur;
cur = cur->left;
}
else if(cur->data == value) //找到了进行删除
{
if (cur->left == 0) //左子树为空
{
if (cur == _root)
{
_root = cur->right;
}
else
{
if (cur == pre->left)
{
pre->left = cur->right;
}
else if (cur == pre->right)
{
pre->right = cur->right;
}
}
destroy_node(cur);
--sizes;
return;
}
else if (cur->right == 0) //右子树为空
{
if (cur == _root) //是根节点的情况
{
_root = cur->left;
}
else
{
if (cur == pre->left)
{
pre->left = cur->left;
}
else
{
pre->right = cur->left;
}
}
destroy_node(cur);
--sizes;
return;
}
else //左右节点都不为空
{
//找右子树的最小节点
node* tmp = cur->right; //右子树最小节点
node* pre2 = cur; //右子树最小节点的父亲
while (tmp->left)
{
pre2 = tmp;
tmp = tmp->left;
}
if (tmp == pre2->left) //分两种情况,第一种是cur != pre2,即右子树有多个节点
{
pre2->left = tmp->right;
}
else //第二种是cur == pre2,即右子树只有一个节点
{
pre2->right = tmp->right;
}
cur->data = tmp->data; //更换节点数据
destroy_node(tmp); //删除右子树最小节点
--sizes;
return;
}
}
}
}
//清空
void clear()
{
if (_root == 0)
{
return;
}
destroy_tree(_root);
sizes = 0;
}
//返回元素数量法
size_t size()const
{
return sizes;
}
//返回树的最大值
const _Ty& max_value()const
{
node* tmp = _root;
for (; tmp!=0;)
{
if (tmp->right == 0)
{
break;
}
tmp = tmp->right;
}
return tmp->data;
}
//返回树的最小值
const _Ty& min_value()const
{
node* tmp = _root;
for (; tmp != 0;)
{
if (tmp->left == 0)
{
break;
}
tmp = tmp->left;
}
return tmp->data;
}
//查找元素法
bool find(const _Ty& value)
{
node* tmp = _find(_root, value);
return tmp == 0 ? 0 : 1;
}
protected:
//树节点申请内存
static node* allocate_node()
{
node * tmp = static_cast<node*>(operator new(sizeof(node)));
tmp->left = 0;
tmp->right = 0;
return tmp;
}
//树节点内存构造元素
static void construct_node(node* ptr, const _Ty& value)
{
construct_at(&ptr->data, value);
}
//析构并摧毁树节点内存
static void destroy_node(node* ptr)
{
destroy_at(&ptr->data);
operator delete(ptr);
}
//删除树的方法,使用递归删除法
void destroy_tree(node* p)
{
if (p == 0)
{
return;
}
destroy_tree(p->left);
destroy_tree(p->right);
destroy_node(p);
}
//拷贝树的方法,递归拷贝
node* copy_tree(node*p)
{
if (p == 0)
{
return 0;
}
node* cpnode = allocate_node();
construct_node(cpnode, p->data);
cpnode->left = copy_tree(p->left);
cpnode->right = copy_tree(p->right);
return cpnode;
}
//内部使用的查找指定的元素节点法
node* _find(node* p,const _Ty& value)
{
if (p == 0)
{
return 0;
}
if (p->data == value)
{
return p;
}
else if(p->data > value)
{
return _find(p->left,value);
}
else if (p->data <= value)
{
return _find(p->right,value);
}
}
private:
node* _root;
size_t sizes;
};


Comments NOTHING